分解性别工资差距#
在本 Notebook 中,我们研究了真实人口普查数据中性别工资差距有多少可以归因于女性和男性在教育或职业上的差异。我们使用了以下论文中的多重稳健因果变化归因方法:>Quintas-Martínez, V., Bahadori, M. T., Santiago, E., Mu, J. and Heckerman, D. “Multiply-Robust Causal Change Attribution,” Proceedings of the 41 st International Conference on Machine Learning, Vienna, Austria. PMLR 235, 2024.
读取和准备数据#
我们将使用 2015 年当前人口调查 (CPS) 的数据。应用与 Chernozhukov et al. (2018) 相同的样本限制后,最终样本包含 18,137 名男性和 14,382 名女性受雇个体。
[1]:
import pandas as pd
# Read and prepare data:
df = pd.read_csv('./cps2015.csv')
# LightGBM works best with integer encoding for categorical variables:
educ_int = {'lhs' : 0, 'hsg' : 1, 'sc' : 2, 'cg' : 3, 'ad' : 4}
df['education'] = pd.from_dummies(df[['lhs', 'hsg', 'sc', 'cg', 'ad']])
df['education'] = df['education'].replace(educ_int)
df = df[['female', 'education', 'occ2', 'wage', 'weight']]
df.columns = ['female', 'education', 'occupation', 'wage', 'weight']
df[['education', 'occupation']] = df[['education', 'occupation']].astype('category')
# We want to explain the change Male -> Female:
data_old, data_new = df.loc[df.female == 0], df.loc[df.female == 1]
因果模型#
要使用我们的因果变化归因方法,我们需要一个将结果(工资)与解释变量联系起来的因果模型。(实际上,该方法只需要知道一个因果顺序。)我们将使用下面的 DAG
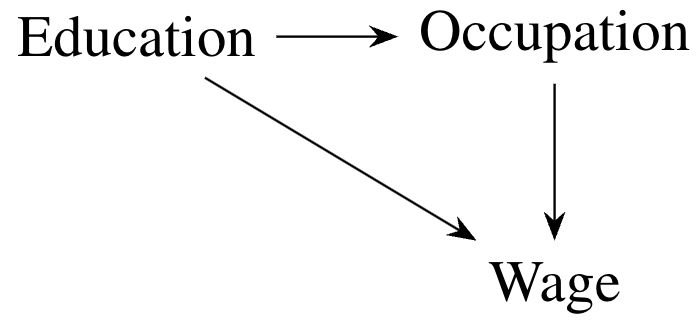
上面的 DAG 意味着数据分布具有以下因果马尔可夫分解
此分解的每个组成部分(DAG 中每个节点在其直接原因下的分布)称为一个因果机制。男性和女性之间工资边际分布的差异可能归因于每个因果机制的差异。我们的目标是将每个机制对总变化的贡献分离开来。
在下面的代码中,我们定义了一个 dowhy.gcm 因果模型
[2]:
import networkx as nx
import dowhy.gcm as gcm
dag = nx.DiGraph([('education', 'occupation'), ('occupation', 'wage'), ('education', 'wage')])
causal_model = gcm.ProbabilisticCausalModel(dag)
使用 dowhy.gcm.distribution_change_robust 实现#
首先,我们展示如何使用 dowhy.gcm.distribution_change_robust 函数计算因果变化归因度量(Shapley 值)。
多重稳健因果变化归因方法基于回归和重新加权方法的组合。在回归方法中,我们在一个样本中学习节点与其父节点之间的依赖关系,然后使用另一个样本的数据来改变该节点的分布。在重新加权方法中,我们对数据进行平均,对那些与目标分布非常相似的观测值赋予更多权重。
默认情况下,dowhy.gcm.distribution_change_robust 使用线性和逻辑回归来学习回归函数和权重。在这里,由于我们的数据集相当大,我们将改用更灵活的算法 HistGradientBoostingRegressor 和 HistGradientBoostingClassifier。
我们还使用 IsotonicRegression 在留出校准样本上校准构成重新加权方法权重的概率。这是可选的,但模拟表明它能提高该方法的性能。
最后,由于我们的数据集很大,我们将使用样本分割(而不是交叉拟合)。也就是说,我们将数据随机分成训练集(用于学习回归和权重)和评估集(用于使用回归和权重计算最终归因度量)。
[3]:
from sklearn.ensemble import HistGradientBoostingRegressor, HistGradientBoostingClassifier
from sklearn.isotonic import IsotonicRegression
from dowhy.gcm.ml.classification import SklearnClassificationModelWeighted
from dowhy.gcm.ml.regression import SklearnRegressionModelWeighted
from dowhy.gcm.util.general import auto_apply_encoders, auto_fit_encoders, shape_into_2d
def make_custom_regressor():
return SklearnRegressionModelWeighted(HistGradientBoostingRegressor(random_state = 0))
def make_custom_classifier():
return SklearnClassificationModelWeighted(HistGradientBoostingClassifier(random_state = 0))
def make_custom_calibrator():
return SklearnRegressionModelWeighted(IsotonicRegression(out_of_bounds = 'clip'))
gcm.distribution_change_robust(causal_model, data_old, data_new, 'wage', sample_weight = 'weight',
xfit = False, calib_size = 0.2,
regressor = make_custom_regressor,
classifier = make_custom_classifier,
calibrator = make_custom_calibrator)
Evaluating set functions...: 100%|██████████| 8/8 [00:02<00:00, 3.77it/s]
[3]:
{'education': 1.1321504485335492,
'occupation': -2.0786979433836734,
'wage': -6.809529336261436}
该函数返回一个字典,其中每个值是对应于键的因果机制的 Shapley 值因果归因度量。(关于 Shapley 值的正式定义,请参见研究论文。)我们将在本 notebook 的最后一节对结果进行更深入的解释。
手动实现(高级)#
其次,我们展示如何使用 dowhy.gcm.distribution_change_robust.ThetaC 类更直接地实现该方法,该类提供了更高级的功能,包括通过高斯乘子自举计算标准误差(见下文)。
[4]:
from sklearn.model_selection import StratifiedKFold, train_test_split
# Split data into train and test set:
X = df[['education', 'occupation']].values
y = df['wage'].values
T = df['female'].values
w = df['weight'].values
# To get the same train-test split:
kf = StratifiedKFold(n_splits = 2, shuffle = True, random_state = 0)
train_index, test_index = next(kf.split(X, T))
X_train, X_eval, y_train, y_eval, T_train, T_eval = X[train_index], X[test_index], y[train_index], y[test_index], T[train_index], T[test_index]
w_train, w_eval = w[train_index], w[test_index]
X_calib, X_train, _, y_train, T_calib, T_train, w_calib, w_train = train_test_split(X_train, y_train, T_train, w_train,
train_size = 0.2, stratify = T_train, random_state = 0)
[5]:
import itertools
from dowhy.gcm.distribution_change_robust import ThetaC
import numpy as np
from math import comb
# All combinations of 0s and 1s, needed for Shapley Values:
all_combos = [list(i) for i in itertools.product([0, 1], repeat=3)]
all_combos_minus1 = [list(i) for i in itertools.product([0, 1], repeat=2)]
# Dictionary to store the multiply-robust scores, will be used later for bootstrap:
scores = {}
# Here we compute the theta^c parameters that make up the Shapley Values (see paper):
for C in all_combos:
scores[''.join(str(x) for x in C)] = ThetaC(C).est_scores(
X_eval,
y_eval,
T_eval,
X_train,
y_train,
T_train,
w_eval=w_eval,
w_train=w_train,
X_calib=X_calib,
T_calib=T_calib,
w_calib=w_calib,
regressor = make_custom_regressor,
classifier = make_custom_classifier,
calibrator = make_custom_calibrator)
# This function combines the theta^c parameters to obtain Shapley values:
w_sort = np.concatenate((w_eval[T_eval==0], w_eval[T_eval==1])) # Order weights in same way as scores
def compute_attr_measure(res_dict, path=False):
# Alternative to Shapley Value: along-a-causal-path (see paper)
if path:
path = np.zeros(3)
path[0] = np.average(res_dict['100'], weights=w_sort) - np.average(res_dict['000'], weights=w_sort)
path[1] = np.average(res_dict['110'], weights=w_sort) - np.average(res_dict['100'], weights=w_sort)
path[2] = np.average(res_dict['111'], weights=w_sort) - np.average(res_dict['110'], weights=w_sort)
return path
# Shapley values:
else:
shap = np.zeros(3)
for k in range(3):
sv = 0.0
for C in all_combos_minus1:
C1 = np.insert(C, k, True)
C0 = np.insert(C, k, False)
chg = (np.average(res_dict[''.join(map(lambda x : str(int(x)), C1))], weights=w_sort) -
np.average(res_dict[''.join(map(lambda x : str(int(x)), C0))], weights=w_sort))
sv += chg/(3*comb(2, np.sum(C)))
shap[k] = sv
return shap
shap = compute_attr_measure(scores, path=False)
shap # Should coincide with the above
[5]:
array([ 1.13215045, -2.07869794, -6.80952934])
由于多重稳健性特性,我们可以使用一种快速的自举方法计算标准误差,该方法无需在每次自举迭代时重新估计回归和权重。相反,我们只需使用独立同分布的正态(0, 1) 抽取值对数据进行重新加权。
[6]:
w_sort = np.concatenate((w_eval[T_eval==0], w_eval[T_eval==1])) # Order weights in same way as scores
def mult_boot(res_dict, Nsim=1000, path=False):
thetas = np.zeros((8, Nsim))
attr = np.zeros((3, Nsim))
for s in range(Nsim):
np.random.seed(s)
new_scores = {}
for k, x in res_dict.items():
new_scores[k] = x + np.random.normal(0,1, X_eval.shape[0])*(x - np.average(x, weights=w_sort))
thetas[:, s] = np.average(np.array([x for k, x in new_scores.items()]), axis=1, weights=w_sort)
attr[:, s] = compute_attr_measure(new_scores, path)
return np.std(attr, axis=1)
shap_se = mult_boot(scores, path=False)
shap_se
[6]:
array([0.34144275, 0.35141792, 0.35805933])
我们可以将结果可视化地呈现在图表中,就像论文中一样
[7]:
from scipy.stats import norm
from statsmodels.stats.weightstats import DescrStatsW
from matplotlib.patches import Rectangle
import matplotlib.pyplot as plt
# Significance stars:
def star(est, se):
if np.abs(est/se)<norm.ppf(.95): # 10%
return ''
elif np.abs(est/se)<norm.ppf(.975): # 5%
return '*'
elif np.abs(est/se)<norm.ppf(.995): # 1%
return '**'
else:
return '***'
# Unconditional wage gap:
stats0 = DescrStatsW(y_eval[T_eval==0], weights=w_eval[T_eval==0], ddof=0)
stats1 = DescrStatsW(y_eval[T_eval==1], weights=w_eval[T_eval==1], ddof=0)
wagegap = (stats1.mean - stats0.mean)
wagegap_se = np.sqrt(stats1.std_mean**2 + stats0.std_mean**2)
# Plot
nam = ["P(educ)", "P(occup | educ)", "P(wage | occup, educ)"]
crit = norm.ppf(.975) # 5% critical value (for error bars)
stars = [star(est, se) for est, se in zip(shap, shap_se)]
fig, ax = plt.subplots()
ax.axvline(x = 0, color='lightgray', zorder=0)
fig.set_size_inches(7, 4)
color = 'C1'
ax.add_patch(Rectangle((0, 4.75), width = wagegap, height = 0.5, color=color, alpha=0.8))
ax.plot((wagegap-crit*wagegap_se, wagegap+crit*wagegap_se,), (5.0, 5.0), color='darkslategray', marker='|', solid_capstyle='butt')
ax.axhline(y = 5.0, color='lightgray', linestyle='dotted', zorder=0)
for i in range(len(shap)):
pos = (shap[i], 3-i+0.25) if shap[i] < 0 else (0, 3-i+0.25)
width = np.abs(shap[i])
ax.add_patch(Rectangle(pos, width = width, height = 0.5, color=color, alpha=0.8))
ax.axhline(y = 3+0.5-i, color='lightgray', linestyle='dotted', zorder=0)
ax.plot((shap[i]-crit*shap_se[i], shap[i]+crit*shap_se[i]), (3-i+0.5, 3-i+0.5), color='darkslategray', marker='|', solid_capstyle='butt')
plt.yticks([5.0] + [3+0.5-i for i in range(3)], [f'Unconditional Wage Gap: {wagegap:.2f}*** ({wagegap_se:.2f})'] +
["{}: {:.2f}{} ({:.2f})".format(nam[i], shap[i], stars[i], shap_se[i]) for i in range(3)])
plt.xlabel('Gender Wage Gap ($/hour)')
plt.show()
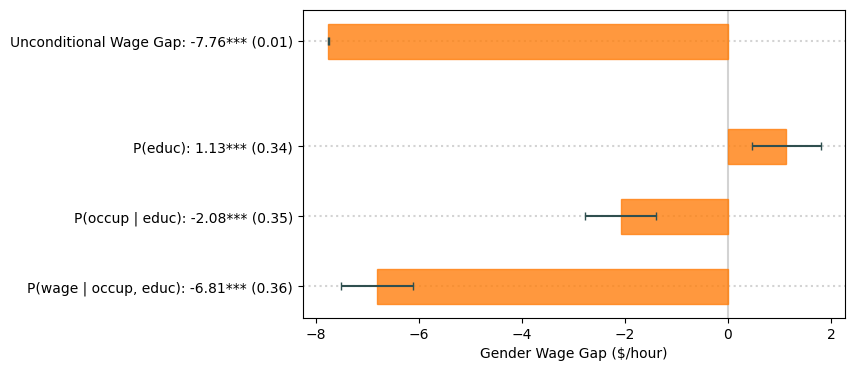
解释#
首先,请注意 \(P(\mathtt{educ})\)、\(P(\mathtt{occup} \mid \mathtt{educ})\) 和 \(P(\mathtt{wage} \mid \mathtt{occup}, \mathtt{educ})\) 的 Shapley 值加起来等于总效应。
其次,\(P(\mathtt{educ})\) 的 Shapley 值为正且具有统计学意义。解释这一度量的一种方式是,如果男性和女性仅在 \(P(\mathtt{educ})\) 上存在差异(但他们的其他因果机制相同),女性平均每小时将比男性多赚 1.13 美元。相反,\(P(\mathtt{occup} \mid \mathtt{educ})\) 的 Shapley 值为负,具有统计学意义,且幅度大于第一个 Shapley 值,因此抵消了教育差异的影响。这些效应衡量两件事:1. 男性与女性之间的因果机制有多大差异?2. 因果机制对结果有多重要?
第三,大部分无条件工资差距归因于因果机制 \(P(\mathtt{wage} \mid \mathtt{occup}, \mathtt{educ})\)。这可以用多种方式解释:1. 未解释的变异:可能存在我们未测量的其他相关变量,这些变量被包含在 \(P(\mathtt{wage} \mid \mathtt{occup}, \mathtt{educ})\) 中。例如,男性和女性之间可能存在 CPS 数据中未测量的经验差异。请注意,这并不会影响我们对其他 Shapley 值的计算结果,因为经验不是教育或职业的直接原因。2. 结构性差异:另一种解释是,由于某种原因(可能或不包括歧视),具有相同可观测特征的女性和男性的工资不同。
下面我们尝试用一些图表来解释这一点。首先,请注意女性的教育水平往往高于男性。相比之下,大学毕业生平均每小时比高中毕业生多赚 12.60 美元。
[8]:
w0, w1 = w_eval[T_eval==0], w_eval[T_eval==1]
data_male_eval = pd.DataFrame({'education' : X_eval[:,0][T_eval==0],
'occupation' : X_eval[:,1][T_eval==0],
'wage' : y_eval[T_eval==0]})
data_female_eval = pd.DataFrame({'education' : X_eval[:,0][T_eval==1],
'occupation' : X_eval[:,1][T_eval==1],
'wage' : y_eval[T_eval==1]})
educ_names = {0 : 'Less than HS', 1 : 'HS Graduate', 2 : 'Some College', 3 : 'College Graduate', 4 : 'Advanced Degree'}
data_male_eval['education'] = data_male_eval['education'].replace(educ_names)
data_female_eval['education'] = data_female_eval['education'].replace(educ_names)
cats_educ = [educ_names[i] for i in range(5)]
ind = np.arange(len(cats_educ))
share0, share1 = np.zeros(len(cats_educ)), np.zeros(len(cats_educ))
for i, c in enumerate(cats_educ):
share0[i] = np.sum(w0*(data_male_eval['education'] == c))/np.sum(w0)*100
share1[i] = np.sum(w1*(data_female_eval['education'] == c))/np.sum(w1)*100
fig = plt.figure()
fig.set_size_inches(6, 5)
plt.bar(ind, share0, 0.4, label='Male')
plt.bar(ind+0.4, share1, 0.4, label='Female')
plt.xticks(ind+0.2, cats_educ, rotation=20, ha='right')
plt.ylabel('Relative Frequency (%)')
plt.xlabel('Education')
plt.legend()
plt.show()
# College graduates vs. high school graduates
diff = (np.average(df[df['education'] == 3]['wage'], weights=df[df['education'] == 3]['weight']) -
np.average(df[df['education'] == 1]['wage'], weights=df[df['education'] == 1]['weight']))
print(f"College vs. HS: {diff:.2f}")
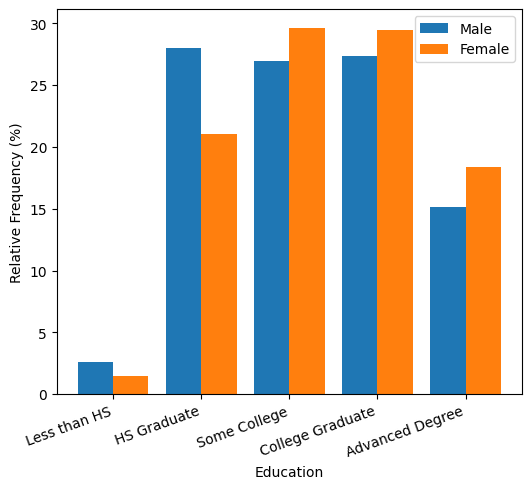
College vs. HS: 12.60
拥有大学学位的女性在行政、教育或医疗保健职业中占主导地位,而拥有大学学位的男性更有可能从事管理或销售工作。相比之下,管理人员平均每小时比教育工作者多赚 16.66 美元,比医疗保健从业者多赚 6.29 美元。
然而,与此同时,存在教育或职业无法解释的巨大差异。例如,女性大学毕业生经理平均每小时比男性同行少赚 13.77 美元。
[9]:
occup_names= {1 : 'Management', 2 : 'Business/Finance', 3 : 'Computer/Math', 4 : 'Architecture/Engineering', 5 : 'Life/Physical/Social Science',
6 : 'Community/Social Sevice', 7 : 'Legal', 8 : 'Education', 9 : 'Arts/Sports/Media', 10 : 'Healthcare Practitioner',
11 : 'Healthcare Support', 12 : 'Protective Services', 13 : 'Food Preparation/Serving', 14 : 'Building Cleaning/Maintenance',
15 : 'Personal Care', 16 : 'Sales', 17 : 'Administrative', 18: 'Farming/Fishing/Forestry', 19 : 'Construction/Mining',
20 : 'Installation/Repairs', 21 : 'Production', 22 : 'Transportation'}
data_male_eval['occupation'] = data_male_eval['occupation'].replace(occup_names)
data_female_eval['occupation'] = data_female_eval['occupation'].replace(occup_names)
cats_occu = ['Management', 'Sales', 'Administrative', 'Education', 'Healthcare Practitioner', 'Other']
ind = np.arange(len(cats_occu))
share0, share1 = np.zeros(len(cats_occu)), np.zeros(len(cats_occu))
for i, c in enumerate(cats_occu[:-1]):
share0[i] = np.sum(w0*((data_male_eval['occupation'] == c) & (data_male_eval['education'] ==
'College Graduate')))/np.sum(w0 * (data_male_eval['education'] ==
'College Graduate'))*100
share1[i] = np.sum(w1*((data_female_eval['occupation'] == c) & (data_female_eval['education'] ==
'College Graduate')))/np.sum(w1 * (data_female_eval['education'] ==
'College Graduate'))*100
share0[-1] = np.sum(w0*((~data_male_eval['occupation'].isin(cats_occu[:-1])) & (data_male_eval['education'] ==
'College Graduate')))/np.sum(w0 * (data_male_eval['education'] ==
'College Graduate'))*100
share1[-1] = np.sum(w1*((~data_female_eval['occupation'].isin(cats_occu[:-1])) & (data_female_eval['education'] ==
'College Graduate')))/np.sum(w1 * (data_female_eval['education'] ==
'College Graduate'))*100
fig = plt.figure()
fig.set_size_inches(6, 5)
plt.bar(ind, share0, 0.4, label='Male')
plt.bar(ind+0.4, share1, 0.4, label='Female')
plt.xticks(ind+0.2, cats_occu, rotation=20, ha='right')
plt.ylabel('Relative Frequency (%)')
plt.xlabel('Occupation | College Graduate')
plt.legend()
plt.show()
# Managers vs. Education
diff = (np.average(df[df['occupation'] == 1]['wage'], weights=df[df['occupation'] == 1]['weight']) -
np.average(df[df['occupation'] == 8]['wage'], weights=df[df['occupation'] == 8]['weight']))
print(f"Management vs. Education: {diff:.2f}")
# Managers vs. Healthcare
diff = (np.average(df[df['occupation'] == 1]['wage'], weights=df[df['occupation'] == 1]['weight']) -
np.average(df[df['occupation'] == 10]['wage'], weights=df[df['occupation'] == 10]['weight']))
print(f"Management vs. Healthcare: {diff:.2f}")
# Female vs. Male College Managers
diff = (np.average(data_female_eval[np.logical_and(data_female_eval['occupation'] == 'Management', data_female_eval['education'] == 'College Graduate')]['wage'],
weights=w1[np.logical_and(data_female_eval['occupation'] == 'Management', data_female_eval['education'] == 'College Graduate')]) -
np.average(data_male_eval[np.logical_and(data_male_eval['occupation'] == 'Management', data_male_eval['education'] == 'College Graduate')]['wage'],
weights=w0[np.logical_and(data_male_eval['occupation'] == 'Management', data_male_eval['education'] == 'College Graduate')]))
print(f"Female vs. Male College Managers: {diff:.2f}")
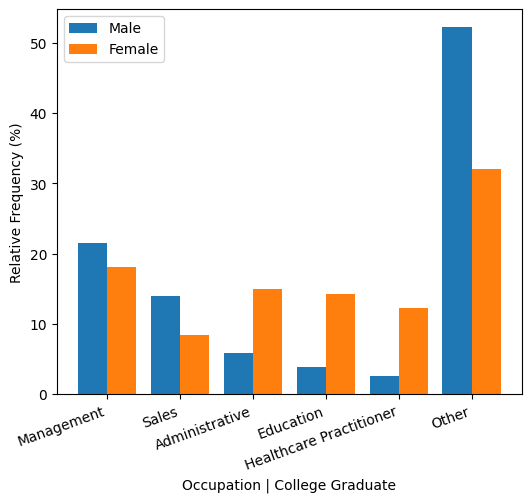
Management vs. Education: 16.66
Management vs. Healthcare: 6.29
Female vs. Male College Managers: -13.77
[ ]: