在 DoWhy 中测试模型假设:一个简单示例#
这是关于如何在 DoWhy 中测试我们假设的图是否正确以及假设是否与数据集匹配的快速介绍。我们通过检查图中的条件独立性来验证它们是否也适用于数据。目前,我们使用偏相关检验连续数据,使用条件互信息检验离散数据。
首先,让我们加载所有必需的软件包。
[1]:
%load_ext autoreload
%autoreload 2
[2]:
import numpy as np
import pandas as pd
import os, sys
sys.path.append(os.path.abspath("../../../"))
import dowhy
from dowhy import CausalModel
import dowhy.datasets
步骤 1:加载数据集#
函数 dataset_from_random_graph(num_vars, num_samples, prob_edge, random_seed, prob_type_data) 可用于从随机生成的有向图创建数据集。数据可以是离散、二元和连续变量的混合。参数具有以下含义: - num_vars:数据集中的变量数 - num_samples:数据集中的样本数 - prob_edge:图中两个随机节点之间存在边的概率 - random_seed:生成随机图的种子 - prob_type_of_data:包含数据分别为离散、二元和连续的概率的 3 元素元组(总和应为 1)
[3]:
data = dowhy.datasets.dataset_from_random_graph(num_vars = 10,
num_samples = 5000,
prob_edge = 0.3,
random_seed = 100,
prob_type_of_data = (0.333, 0.333, 0.334))
df = data["df"] #Insert dataset here
print(data["discrete_columns"], data["continuous_columns"], data["binary_columns"])
print(df.head())
['a', 'c', 'e', 'f', 'h'] ['b', 'd', 'g', 'i', 'j'] ['c', 'e']
a b c d e f g h i j
0 -1 -1.170054 1 0.996507 1 0 -0.218214 -1 -1.107993 0.699933
1 0 0.527130 1 0.894435 1 1 1.485562 0 -1.450727 -1.055649
2 0 0.436049 0 -0.151908 0 0 0.195296 0 2.280391 1.162284
3 0 0.005213 1 0.347139 1 0 -0.727156 -1 -1.140999 -2.165819
4 0 1.212397 0 -1.230150 0 1 0.582913 0 -1.377051 -2.359753
请注意,我们使用 pandas dataframe 来加载数据。目前,DoWhy 只支持将 pandas dataframe 作为输入。
步骤 2:输入因果图#
现在我们输入一个因果图。您可以使用 GML 图格式(推荐)、DOT 格式或 daggity 的输出来完成。要为您的数据集创建因果图,您可以使用像 DAGitty 这样的工具,它提供图形用户界面来构建图。您可以导出它生成的图字符串。
[4]:
graph_string = """graph [
directed 1
node [
id 0
label "a"
]
node [
id 1
label "b"
]
node [
id 2
label "c"
]
node [
id 3
label "d"
]
node [
id 4
label "e"
]
node [
id 5
label "f"
]
node [
id 6
label "g"
]
node [
id 7
label "h"
]
node [
id 8
label "i"
]
node [
id 9
label "j"
]
edge [
source 0
target 1
]
edge [
source 0
target 8
]
edge [
source 1
target 2
]
edge [
source 1
target 5
]
edge [
source 2
target 3
]
edge [
source 2
target 4
]
edge [
source 3
target 4
]
edge [
source 4
target 5
]
edge [
source 5
target 6
]
edge [
source 6
target 7
]
edge [
source 7
target 8
]
edge [
source 8
target 9
]
]
"""
步骤 3:创建因果模型#
[5]:
model=CausalModel(
data = df,
treatment=data["treatment_name"],
outcome=data["outcome_name"],
graph=graph_string
)
[6]:
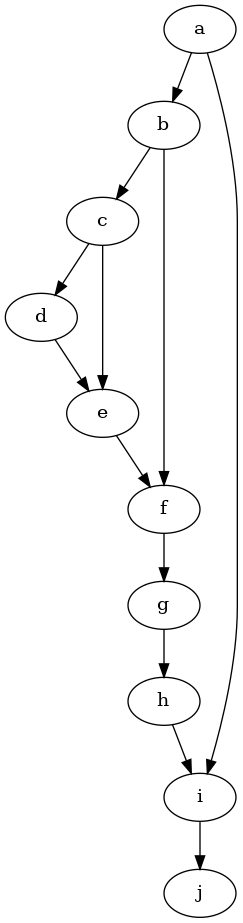
model.view_model()
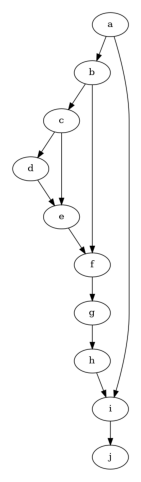
[7]:
from IPython.display import Image, display
display(Image(filename="causal_model.png"))
步骤 4:检验条件独立性#
我们可以使用 model.refute_graph(k, independence_test = {'test_for_continuous': 'partial_correlation', 'test_for_discrete' : 'conditional_mutual_information'}) 检查图的假设是否适用于数据。我们正在检验 X ⫫ Y | Z,其中 X 和 Y 是单例集,Z 可以包含 k 个变量。除非另有输入,否则 k 值默认为 1。目前我们使用以下设置: - 连续数据的“partial_correlation” - 离散数据的“conditional_mutual_information” - 当 Z 为离散且 X 和 Y 中任一为连续时的“conditional_mutua_information” - 当 Z 为连续/二元且 X 和 Y 为连续/二元时的“partial_correlation” - 当 X 和 Y 为离散且 Z 包含混合数据时的“conditional_mutual_information” - 当前不支持其他设置
[8]:
refuter_object = model.refute_graph(k=1, independence_test = {'test_for_continuous': 'partial_correlation', 'test_for_discrete' : 'conditional_mutual_information'}) #Change k parameter to test conditional independence given different number of variables
[9]:
print(refuter_object)
Method name for discrete data:conditional_mutual_information
Method name for continuous data:partial_correlation
Number of conditional independencies entailed by model:34
Number of independences satisfied by data:25
Test passed:True
检验一组边#
我们还可以检验一组条件独立性是否为真。输入必须是以下形式: - [( x1, y1, (z1, z2)), ( x2, y2, (z3, z4)), ( x3, y3, (z5,)), ( x4, y4, ()) ] ##### 检验数据也可以是离散和连续类型的混合(这里二元仅指离散) -
[10]:
refuter_object = model.refute_graph(independence_constraints = [('c', 'e' , ('g',)), # c and e - binary, g - continuous
('f', 'h' , ('b',)), # f and h - discrete, b - continuous
('e', 'g' , ('h',)), # e - binary, g - continuous, h - discrete
('c', 'a' , ('b',)), # c and a - discrete, b - continuous
('d', 'i' , ('c',)), # d and i - continuous, c - binary
('a', 'j' , ()) # a - discrete, j - continuous
],
independence_test = {'test_for_continuous': 'partial_correlation', 'test_for_discrete' : 'conditional_mutual_information'}
)
[11]:
print(refuter_object)
Method name for discrete data:conditional_mutual_information
Method name for continuous data:partial_correlation
Number of conditional independencies entailed by model:6
Number of independences satisfied by data:6
Test passed:True
使用错误的图输入进行检验#
[12]:
graph_string = """graph [
directed 1
node [
id 0
label "a"
]
node [
id 1
label "b"
]
node [
id 2
label "c"
]
node [
id 3
label "d"
]
node [
id 4
label "e"
]
node [
id 5
label "f"
]
node [
id 6
label "g"
]
node [
id 7
label "h"
]
node [
id 8
label "i"
]
node [
id 9
label "j"
]
edge [
source 0
target 1
]
edge [
source 0
target 2
]
edge [
source 0
target 3
]
edge [
source 1
target 4
]
edge [
source 1
target 5
]
edge [
source 2
target 3
]
edge [
source 4
target 2
]
edge [
source 4
target 5
]
edge [
source 4
target 6
]
edge [
source 4
target 7
]
edge [
source 8
target 6
]
edge
[
source 9
target 0
]
]"""
[13]:
model = CausalModel(
data=df,
treatment=data["treatment_name"],
outcome=data["outcome_name"],
graph=graph_string,
)
[14]:
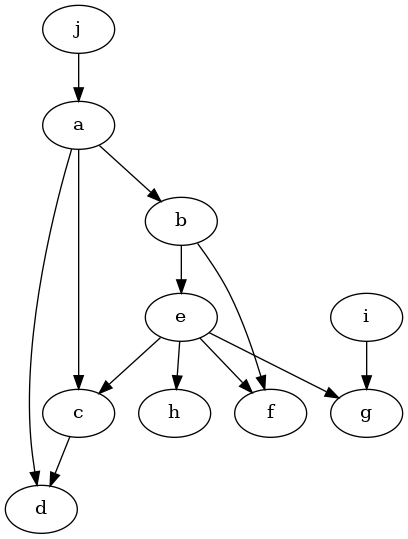
model.view_model()
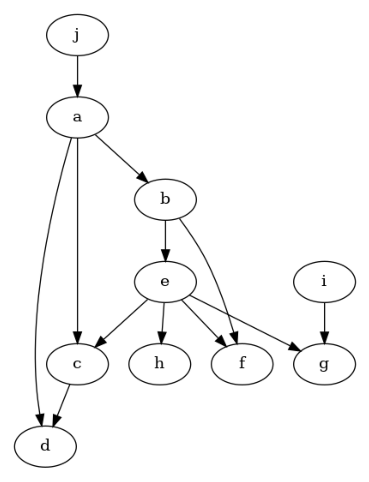
[15]:
from IPython.display import Image, display
display(Image(filename="causal_model.png"))
[16]:
refuter_object = model.refute_graph(k=2)
我们可以看到,由于我们输入了错误的图,许多条件独立性未能满足。
[17]:
print(refuter_object)
Method name for discrete data:conditional_mutual_information
Method name for continuous data:partial_correlation
Number of conditional independencies entailed by model:359
Number of independences satisfied by data:144
Test passed:False
[ ]: