图拒绝

为了检验完整图的有效性，我们需要检验图中隐含的每个条件独立性约束，这些约束被称为局部马尔可夫条件 (LMC)。为了检验图的有效性，我们可以编写

>>> from dowhy.gcm.falsify import falsify_graph
>>> # causal_graph is a networkx digraph
>>> result = falsify_graph(causal_graph, data, show_progress_bar=False)
>>> print(result)

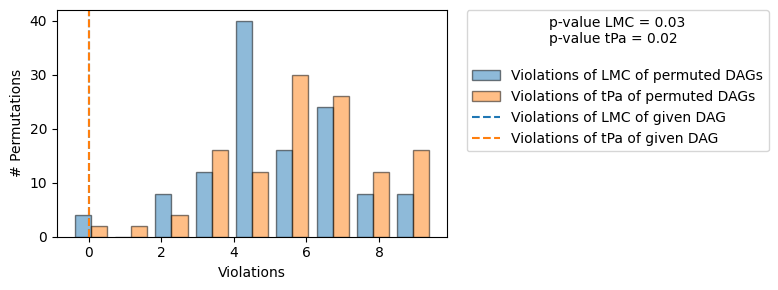
falsify_graph 的结果显示了两个测试的输出。第一个测试衡量图中隐含的 LMC 是否被数据满足。它将给定图违反的 LMC 数量与随机图违反的 LMC 数量进行比较。对于 0.05 的显著性水平，如果给定图违反的 LMC 数量低于 5% 的最佳随机图，则我们不拒绝该图。第二个测试 (tPa) 检查图是否可证伪。也就是说，假设给定图是正确的，有多少其他图违反 LMC 的数量相同？由于假定该图是正确的，因此正确的 LMC 是图中隐含的 LMC，因此违反的参考数量为零。对于 0.05 的显著性水平，如果少于 5% 的随机图违反 LMC 的数量为零，则表明图中隐含的 LMC 可以证伪（或驳斥）该图。

如果我们只想知道图是否可证伪，我们可以直接查询结果对象。

>>> print(f"Graph is falsifiable: {result.falsifiable}, Graph is falsified: {result.falsified}")

有关使用 falsify_graph 驳斥图的更多详细信息，请查看关于驳斥 DAGs 的 notebook。