归因分布变化#

在归因分布变化时，我们回答这个问题：

我的系统中，在两组数据之间，哪个机制发生了变化？换句话说，我的数据中哪个节点的行为不同了？

在这里，我们想要识别图中因果机制发生变化的一个或多个节点。例如，如果在微服务架构中检测到应用程序延迟增加，我们的目标是识别行为发生改变的节点/组件。DoWhy 实现了一种方法，根据以下论文，将分布的变化归因于上游节点因果机制的变化：

Kailash Budhathoki, Dominik Janzing, Patrick Blöbaum, Hoiyi Ng. 分布为什么会改变？ Proceedings of The 24th International Conference on Artificial Intelligence and Statistics, PMLR 130:1666-1674, 2021.

此外，为了解释目标变量均值（或其他类似均值的汇总统计量）的变化，DoWhy 实现了一种多重稳健因果变化归因方法，该方法结合了回归和重新加权，使最终估计对估计误差的敏感性降低。该方法在以下论文中提出：

Victor Quintas-Martinez, Mohammad Taha Bahadori, Eduardo Santiago, Jeff Mu, David Heckerman. 多重稳健因果变化归因 Proceedings of the 41st International Conference on Machine Learning, PMLR 235:41821–41840, 2024.

如何使用#

为了了解如何使用该方法，让我们以上述微服务示例为例，假设我们有一个由四个服务 \(X, Y, Z, W\) 组成的系统，每个服务都监控延迟。假设我们计划进行一次新的部署，并记录部署前后的延迟。我们将部署前收集的延迟数据称为 data_old，将部署后收集的数据称为 data_new

>>> import networkx as nx, numpy as np, pandas as pd
>>> from dowhy import gcm
>>> from scipy.stats import halfnorm

>>> X = halfnorm.rvs(size=1000, loc=0.5, scale=0.2)
>>> Y = halfnorm.rvs(size=1000, loc=1.0, scale=0.2)
>>> Z = np.maximum(X, Y) + np.random.normal(loc=0, scale=0.5, size=1000)
>>> W = Z + halfnorm.rvs(size=1000, loc=0.1, scale=0.2)
>>> data_old = pd.DataFrame(data=dict(X=X, Y=Y, Z=Z, W=W))

>>> X = halfnorm.rvs(size=1000, loc=0.5, scale=0.2)
>>> Y = halfnorm.rvs(size=1000, loc=1.0, scale=0.2)
>>> Z = X + Y + np.random.normal(loc=0, scale=0.5, size=1000)
>>> W = Z + halfnorm.rvs(size=1000, loc=0.1, scale=0.2)
>>> data_new = pd.DataFrame(data=dict(X=X, Y=Y, Z=Z, W=W))

在这里，我们改变了 \(Z\) 的行为，这模拟了多线程代码意外转换为顺序执行（并行等待 \(X\) 和 \(Y\) 与顺序等待它们）。这将改变 \(Z\) 的分布，并随后改变 \(W\) 的分布。

接下来，我们将因果关系建模为一个概率因果模型

>>> causal_model = gcm.ProbabilisticCausalModel(nx.DiGraph([('X', 'Z'), ('Y', 'Z'), ('Z', 'W')]))  # (X, Y) -> Z -> W
>>> gcm.auto.assign_causal_mechanisms(causal_model, data_old)

最后，我们将 \(W\) 分布的变化归因于因果机制的变化

>>> attributions = gcm.distribution_change(causal_model, data_old, data_new, 'W')
>>> attributions
{'W': 0.012553173521649849, 'X': -0.007493424287710609, 'Y': 0.0013256550695736396, 'Z': 0.7396701922473544}

尽管 \(W\) 的分布也发生了变化，但该方法几乎完全将变化归因于 \(Z\)，而其他变量的得分可以忽略不计。这与我们的预期一致，因为我们只改变了 \(Z\) 的机制。

多重稳健方法的工作原理类似

>>> attributions_robust = gcm.distribution_change_robust(causal_model, data_old, data_new, 'W')
>>> attributions_robust
{W: 0.012386916935751025, X: -0.0002994129507127999, Y: 0.006618489296759587, Z: 0.6448455410771148}

和之前一样，我们估计 \(Z\) 的归因得分很高，而其他变量的得分接近于 0。请注意，归因得分的单位取决于使用的度量（见下一节）。默认情况下，distribution_change 将变化分解为与原始分布的 KL 散度，而 distribution_change_robust 将变化分解为目标节点 \(W\) 的均值变化。

读者可能已经注意到，使用此方法时，不涉及拟合步骤。原因是，此函数会在内部调用 fit。具体来说，此函数将创建因果图的两个副本，并将一个图拟合到第一个数据集，将第二个图拟合到第二个数据集。

理解该方法#

这些方法背后的思想是系统地用基于新数据集学习到的机制替换基于旧数据集学习到的因果机制。每次替换后，都会为目标节点生成新的样本，其中数据生成过程是旧机制和新机制的混合。我们的目标是识别发生变化的机制，这将导致目标变量的边际分布发生变化，而未改变的机制将导致相同的边际分布。为了实现这一点，我们采用 Shapley 对称化的思想来系统地替换机制。这使我们能够识别哪些节点发生了变化，并根据某种度量估计归因得分。请注意，机制的变化可能是由于底层模型的功能变化或（未观察到的）噪声分布的变化。然而，这两种变化都会导致机制的变化。

distribution_change 和 distribution_change_robust 的主要区别在于归因度量的计算方式。distribution_change 首先学习‘旧’数据和‘新’数据中每个节点的条件分布，然后使用这些估计来计算归因度量。distribution_change_robust 不学习整个条件分布，而是学习条件均值（回归）和重要性权重（重新加权），然后将它们结合起来计算归因度量。最后一步，使用 Shapley 值将这些归因度量合并为有意义的得分，这对于两种方法是相同的。

distribution_change 的步骤如下：

从‘旧’数据（例如，部署前的延迟）估计条件分布：\(P_{X_1, ..., X_n} = \prod_j P_{X_j | PA_j}\)，其中 \(P_{X_j | PA_j}\) 是节点 \(X_j\) 的因果机制，\(PA_j\) 是节点 \(X_j\) 的父节点。
从‘新’数据（例如，部署后的延迟）估计条件分布：\(\tilde P_{X_1, ..., X_n} = \prod_j \tilde P_{X_j | PA_j}\)
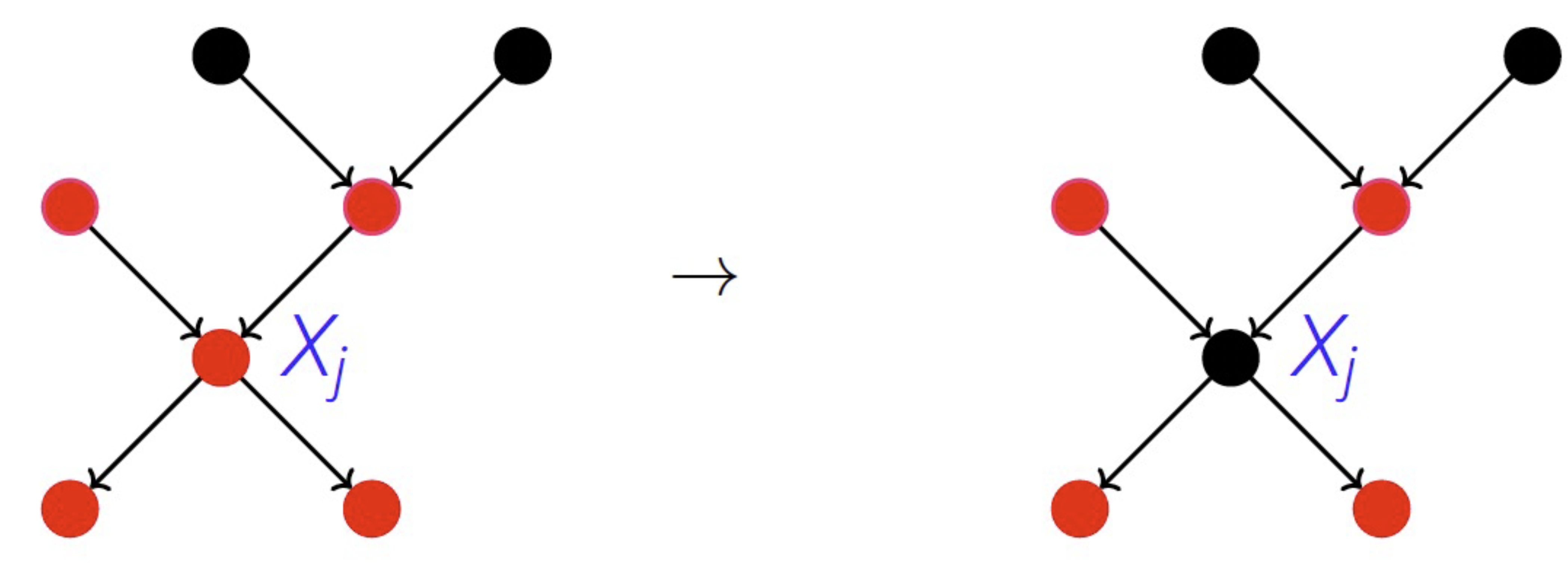
系统地、逐个地用基于‘新’数据的机制替换基于‘旧’数据的机制。为此，将每个 \(j\) 的 \(P_{X_j | PA_j}\) 替换为 \(\tilde P_{X_j | PA_j}\)。如果集合 \(T \subseteq \{1, ..., n\}\) 中的节点之前已被替换，我们将得到 \(\tilde P^{X_n}_T = \sum_{x_1, ..., x_{n-1}} \prod_{j \in T} \tilde P_{X_j | PA_j} \prod_{j \notin T} P_{X_j | PA_j}\)，这是节点 \(n\) 的新边际分布。
使用 Shapley 值，通过比较 \(P^{X_n}_{T \bigcup \{j\}}\) 和 \(P^{X_n}_{T}\)，将给定 \(T\) 时边际分布的变化归因于 \(X_j\)。在这里，我们可以使用不同的度量来衡量变化，例如与原始分布的 KL 散度或方差差等。

有关更详细的解释，请参阅相应论文：分布为什么会改变？

distribution_change_robust 的步骤如下：

学习回归函数：如果希望改变其因果机制，则使用回归算法估计‘新’数据中每个节点与其父节点之间的依赖关系；如果希望保持该节点不变，则使用‘旧’数据中的依赖关系。
学习重要性权重：使用分类算法，我们估计重要性权重，这些权重对特定因果机制更接近‘新’数据的数据点赋予更高的权重。
回归和权重的组合使我们能够估计在分布 \(\tilde P^{X_n}_T = \sum_{x_1, ..., x_{n-1}} \prod_{j \in T} \tilde P_{X_j | PA_j} \prod_{j \notin T} P_{X_j | PA_j}\) 下目标节点的均值，其中集合 \(T \subseteq \{1, ..., n\}\) 中的因果机制已调整为与‘新’数据中的机制相同。
使用 Shapley 值，通过比较 \(P^{X_n}_{T \bigcup \{j\}}\) 和 \(P^{X_n}_{T}\)，将给定 \(T\) 时边际分布的变化归因于 \(X_j\)。

有关更详细的解释，请参阅相应论文：多重稳健因果变化归因

归因分布变化#

如何使用#

相关示例笔记本#

理解该方法#