用户给定有向无环图的证伪#
本 notebook 演示了一个使用观测数据证伪用户给定 DAG 的工具。主要函数是 falsify_graph(),它将 DAG 和数据作为输入并返回评估结果。有关此方法的更多详细信息,请阅读相关论文
Eulig, E., Mastakouri, A. A., Blöbaum, P., Hardt, M., & Janzing, D. (2023)。基于置换检验的因果图证伪研究。《Toward Falsifying Causal Graphs Using a Permutation-Based Test》。https://arxiv.org/abs/2305.09565
[1]:
# Import the necessary libraries and functions for this demo
import numpy as np
import pandas as pd
import networkx as nx
from sklearn.ensemble import GradientBoostingRegressor
from dowhy.gcm.falsify import FalsifyConst, falsify_graph, plot_local_insights, run_validations, apply_suggestions
from dowhy.gcm.independence_test.generalised_cov_measure import generalised_cov_based
from dowhy.gcm.util import plot
from dowhy.gcm.util.general import set_random_seed
from dowhy.gcm.ml import SklearnRegressionModel
from dowhy.gcm.util.general import set_random_seed
set_random_seed(0)
# Set random seed
set_random_seed(1332)
合成数据#
我们首先将在合成数据上演示此工具。为此,我们生成了一个包含 5 个节点的随机 DAG falsify_g_true.gml 和来自具有非线性条件的随机 SCM 的一些数据 (falsify_data_nonlinear.csv)。
[2]:
# Load example graph and data
g_true = nx.read_gml(f"falsify_g_true.gml")
data = pd.read_csv(f"falsify_data_nonlinear.csv")
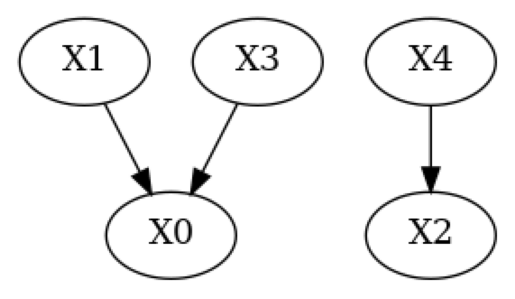
# Plot true DAG
print("True DAG")
plot(g_true)
True DAG
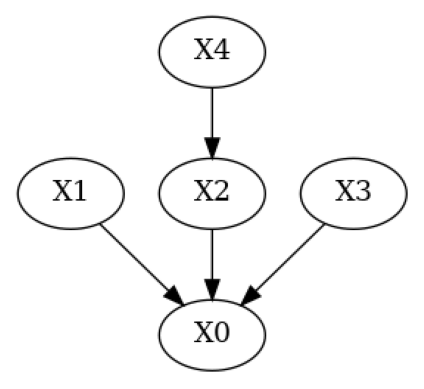
首先,让我们在该数据上评估真实的 DAG(以下单元格运行大约需要 20 秒)
[3]:
result = falsify_graph(g_true, data, plot_histogram=True)
# Summarize the result
print(result)
Test permutations of given graph: 100%|██████████| 20/20 [00:16<00:00, 1.24it/s]
+-------------------------------------------------------------------------------------------------------+
| Falsification Summary |
+-------------------------------------------------------------------------------------------------------+
| The given DAG is informative because 1 / 20 of the permutations lie in the Markov |
| equivalence class of the given DAG (p-value: 0.05). |
| The given DAG violates 0/11 LMCs and is better than 90.0% of the permuted DAGs (p-value: 0.10). |
| Based on the provided significance level (0.05) and because the DAG is informative, |
| we do not reject the DAG. |
+-------------------------------------------------------------------------------------------------------+
正如预期的那样,我们不会拒绝真实的 DAG。让我们了解 falsify_graph() 具体做了什么:当我们向 falsify_graph() 提供一个给定的 DAG 时,我们通过运行条件独立性检验 (CIs) 来测试局部马尔可夫条件 (LMC) 的违规。即,对于图中的每个节点,我们测试是否
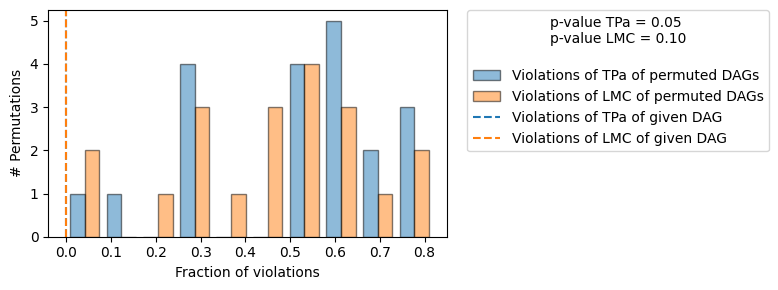
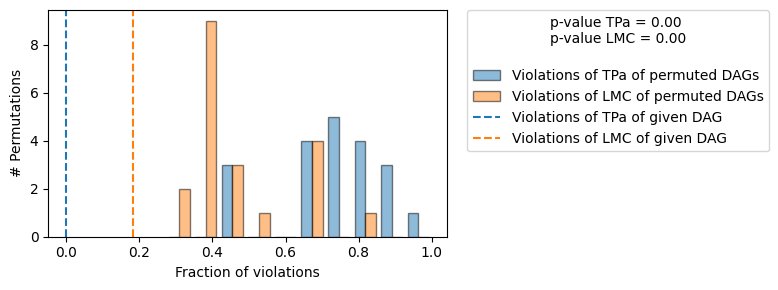
然后,我们随机置换给定 DAG 的节点,并再次测试 LMC 的违规情况。我们可以对固定数量的置换执行此操作,或者对给定 DAG 中的所有 \(n!,n:\) 节点进行置换。然后,我们可以使用随机节点置换(零假设)的违规次数与给定 DAG(检验统计量)一样少或更少的概率,作为验证给定 DAG 的度量(上图右上角报告的 p 值)。
类似地,我们可以对给定 DAG 的每个置换运行一个预言机检验,即,如果给定 DAG 是真实的 DAG,我们期望某些置换有多少 LMC 违规。请注意,询问违反零 LMC 的置换次数与询问有多少 DAG 位于与给定 DAG 相同的马尔可夫等价类 (MEC) 中是相同的。在我们的方法中,我们使用与给定 DAG 位于同一 MEC 中的置换 DAG 的数量(tPA 违规数为 0)作为衡量给定 DAG 信息量的度量。只有当少数置换位于同一 MEC 中时,给定 DAG 所蕴含的独立性才具有“特征性”,这意味着可以通过检验隐含的 CI 来证伪给定 DAG。
在上图中,我们看到置换 DAG 的 LMC 违规(蓝色)和置换 DAG 的 d 分离(预言机,橙色)违规的直方图。橙色和蓝色的虚线表示给定 DAG 的 LMC(蓝色)/d 分离(橙色)违规次数。正如真实的 DAG 所预期的那样,两个直方图大致重叠(CI 检验中的统计误差除外)。
如果我们不关心图而只想知道是否使用我们的检验证伪了给定 DAG,我们可以转而使用 falsify_graph() 返回的 EvaluationResult 对象的 falsified 属性。
[4]:
print(f"Graph is falsifiable: {result.falsifiable}, Graph is falsified: {result.falsified}")
Graph is falsifiable: True, Graph is falsified: False
现在,让我们修改真实的 DAG,模拟一个领域专家知道一些边但删除了一条真实的边并引入了一条错误的边的 DAG。
[5]:
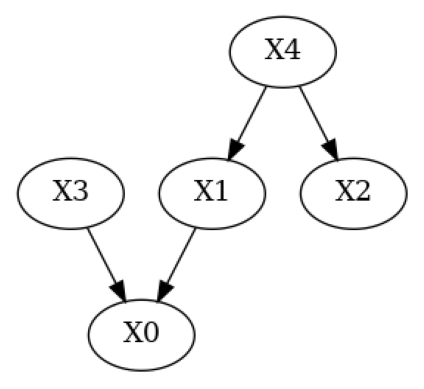
# Simulate a domain expert with knowledge over some of the edges in the system
g_given = g_true.copy()
g_given.add_edges_from(([('X4', 'X1')])) # Add wrong edge from X4 -> X1
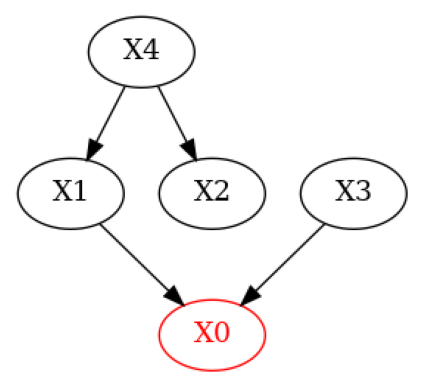
g_given.remove_edge('X2', 'X0') # Remove true edge from X2 -> X0
plot(g_given)
[6]:
# Run evaluation and plot the result using `plot=True`
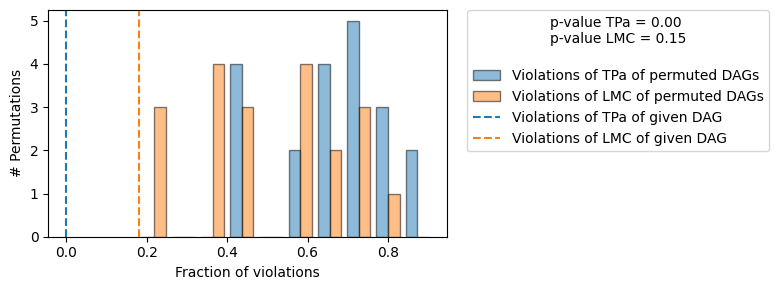
result = falsify_graph(g_given, data, plot_histogram=True)
# Summarize the result
print(result)
Test permutations of given graph: 100%|██████████| 20/20 [00:17<00:00, 1.13it/s]
+-------------------------------------------------------------------------------------------------------+
| Falsification Summary |
+-------------------------------------------------------------------------------------------------------+
| The given DAG is informative because 0 / 20 of the permutations lie in the Markov |
| equivalence class of the given DAG (p-value: 0.00). |
| The given DAG violates 2/11 LMCs and is better than 85.0% of the permuted DAGs (p-value: 0.15). |
| Based on the provided significance level (0.05) and because the DAG is informative, |
| we reject the DAG. |
+-------------------------------------------------------------------------------------------------------+
这里,我们观察到两件事。首先,给定 DAG 比真实 DAG 多违反 2 个 LMC。其次,有许多置换的 DAG 违反的 LMC 次数与给定 DAG 相同或更少。这反映在 LMC 的 p 值中,该值远高于之前。基于默认的显著性水平 0.05,我们将因此拒绝给定 DAG。
通过突出显示给定 DAG 中发生 LMC 违规的节点,我们可以获得更多见解。
[7]:
# Plot nodes for which violations of LMCs occured
print('Violations of LMCs')
plot_local_insights(g_given, result, method=FalsifyConst.VALIDATE_LMC)
Violations of LMCs
真实数据(Sachs 等人于 2005 年发布的蛋白质网络数据集)#
[8]:
# Load the data and consensus DAG
data_url = "https://raw.githubusercontent.com/FenTechSolutions/CausalDiscoveryToolbox/master/cdt/data/resources/cyto_full_data.csv"
data_sachs = pd.read_csv(data_url)
g_sachs = nx.read_gml('falsify_sachs.gml')
[9]:
plot(g_sachs)
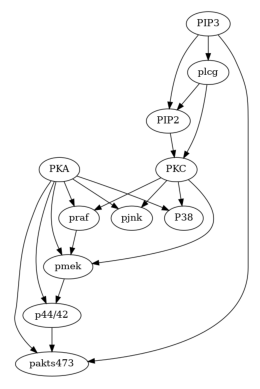
由于样本数量庞大,使用上面的核检验进行评估对于此演示来说耗时太长。因此,我们将转而使用基于广义协方差度量 (GCM) 的检验。我们将使用 sklearn 的梯度提升决策树作为回归器。
[10]:
# Define independence test based on the generalised covariance measure with gradient boosted decision trees as models
def create_gradient_boost_regressor(**kwargs) -> SklearnRegressionModel:
return SklearnRegressionModel(GradientBoostingRegressor(**kwargs))
def gcm(X, Y, Z=None):
return generalised_cov_based(X, Y, Z=Z, prediction_model_X=create_gradient_boost_regressor,
prediction_model_Y=create_gradient_boost_regressor)
对图的所有 11! 节点置换运行我们的基线是不可行的(也是不必要的)。因此,我们将 n_permutations=100 设置为使用 100 个随机置换进行评估。为了使用上面定义的 GCM 检验,我们将使用参数 independence_test=gcm(无条件独立性检验)和 conditional_independence_test=gcm(条件独立性检验)。
以下单元格运行大约需要 3 分钟。
[11]:
# Run evaluation for consensus graph and data.
result_sachs = falsify_graph(g_sachs, data_sachs, n_permutations=100,
independence_test=gcm,
conditional_independence_test=gcm,
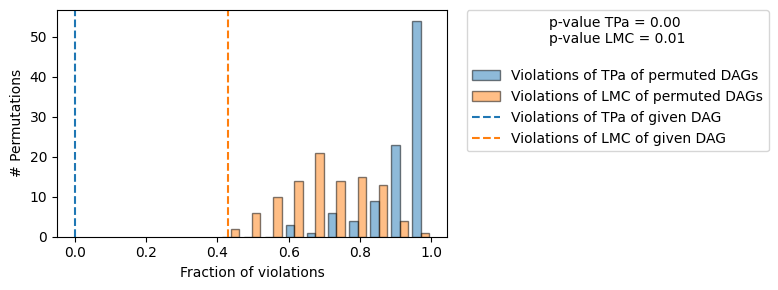
plot_histogram=True)
print(result_sachs)
Test permutations of given graph: 100%|██████████| 100/100 [11:57<00:00, 7.18s/it]
+-------------------------------------------------------------------------------------------------------+
| Falsification Summary |
+-------------------------------------------------------------------------------------------------------+
| The given DAG is informative because 0 / 100 of the permutations lie in the Markov |
| equivalence class of the given DAG (p-value: 0.00). |
| The given DAG violates 21/49 LMCs and is better than 99.0% of the permuted DAGs (p-value: 0.01). |
| Based on the provided significance level (0.05) and because the DAG is informative, |
| we do not reject the DAG. |
+-------------------------------------------------------------------------------------------------------+
我们观察到,共识 DAG 既信息丰富(100 个置换中有 0 个位于同一 MEC 中),并且在蕴含的 CI 方面显著优于随机。请注意,给定 DAG 的 LMC 违规次数远高于此处使用的默认显著性水平 significance_ci=0.05 下 CI 检验的预期第一类错误率。因此,如果采用幼稚的方法,即拒绝 LMC 违规超过 5% 的 DAG,将错误地拒绝此 DAG。
边建议#
除了上面显示的给定 DAG 的证伪之外,我们还可以使用 suggestions=True 运行附加测试,并将结果报告给用户。为了演示这一点,我们将使用之前的合成 DAG 和数据。
[12]:
result = falsify_graph(g_given, data, plot_histogram=True, suggestions=True)
print(result)
Test permutations of given graph: 100%|██████████| 20/20 [00:18<00:00, 1.07it/s]
+-------------------------------------------------------------------------------------------------------+
| Falsification Summary |
+-------------------------------------------------------------------------------------------------------+
| The given DAG is informative because 0 / 20 of the permutations lie in the Markov |
| equivalence class of the given DAG (p-value: 0.00). |
| The given DAG violates 2/11 LMCs and is better than 100.0% of the permuted DAGs (p-value: 0.00). |
| Based on the provided significance level (0.05) and because the DAG is informative, |
| we do not reject the DAG. |
+-------------------------------------------------------------------------------------------------------+
| Suggestions |
+-------------------------------------------------------------------------------------------------------+
| Causal Minimality | - Remove edge X4 --> X1 |
+-------------------------------------------------------------------------------------------------------+
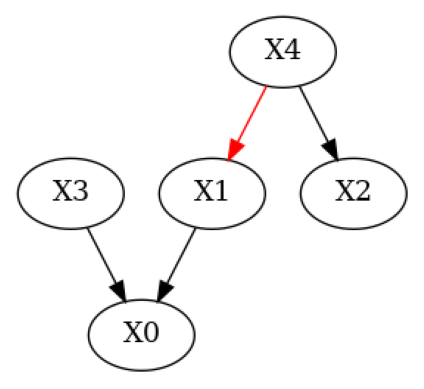
与上面的输出相比,我们现在在评估摘要的打印表示中看到了附加行 Suggestions。我们使用了因果最小性检验来向用户报告建议,并将正确地建议删除边 \(X4 \to X1\),该边是由领域专家错误添加的。我们还可以使用 plot_local_insights 绘制这些建议
[13]:
# Plot suggestions
plot_local_insights(g_given, result, method=FalsifyConst.VALIDATE_CM)
我们可以使用 apply_suggestions 应用这些建议。如果有一些边我们不想删除,我们可以使用附加参数 edges_to_keep 来指定我们不想删除的边。
[14]:
# Apply all suggestions (we could exclude suggestions via `edges_to_keep=[('X3', 'X4')])`)
g_given_pruned = apply_suggestions(g_given, result)
# Plot pruned DAG
plot(g_given_pruned)