异常归因#

当我们在目标节点中观察到异常时，我们可以解决以下问题：

每个上游节点和目标节点对观测到的异常贡献了多少？

通过此方法，我们可以识别并量化每个节点对异常观测的贡献。本方法基于以下论文：

Kailash Budhathoki, Lenon Minorics, Patrick Blöbaum, Dominik Janzing. Causal structure-based root cause analysis of outliers 国际机器学习大会，2022

如何使用#

首先，我们生成一个简单链条 X → Y → Z → W 的示例数据

>>> import numpy as np, pandas as pd, networkx as nx
>>> from dowhy import gcm

>>> X = np.random.uniform(low=-5, high=5, size=1000)
>>> Y = 0.5 * X + np.random.normal(loc=0, scale=1, size=1000)
>>> Z = 2 * Y + np.random.normal(loc=0, scale=1, size=1000)
>>> W = 3 * Z + np.random.normal(loc=0, scale=1, size=1000)
>>> data = pd.DataFrame(data=dict(X=X, Y=Y, Z=Z, W=W))

接下来，我们将因果关系建模为一个可逆的结构因果模型，并将其拟合到数据。我们使用 auto 模块自动分配因果机制。

>>> causal_model = gcm.InvertibleStructuralCausalModel(nx.DiGraph([('X', 'Y'), ('Y', 'Z'), ('Z', 'W')]))  # X -> Y -> Z -> W
>>> gcm.auto.assign_causal_mechanisms(causal_model, data)
>>> gcm.fit(causal_model, data)

然后，我们创建一个异常。例如，我们将 \(Y\) 的噪声设置为异常高的值。

>>> X = np.random.uniform(low=-5, high=5)  # Sample from its normal distribution.
>>> Y = 0.5 * X + 5  # Here, we set the noise of Y to 5, which is unusually high.
>>> Z = 2 * Y
>>> W = 3 * Z
>>> anomalous_data = pd.DataFrame(data=dict(X=[X], Y=[Y], Z=[Z], W=[W]))  # This data frame consist of only one sample here.

在这里，\(Y\) 是根本原因，它导致 \(Y, Z\) 和 \(W\) 出现异常。我们现在可以获取我们感兴趣的目标节点（例如，\(W\)）的异常归因分数。

>>> attribution_scores = gcm.attribute_anomalies(causal_model, 'W', anomaly_samples=anomalous_data)
>>> attribution_scores
    {'X': array([0.59766433]), 'Y': array([7.40955119]), 'Z': array([-0.00236857]), 'W': array([0.0018539])}

虽然我们在这里使用线性关系，但该方法也可以适应任意非线性关系。也可能存在多个根本原因。

结果解释： 我们估计了 \(W\) 的祖先（包括 \(W\) 本身）对观测到的异常的贡献。虽然所有节点都有一定程度的贡献，但 \(Y\) 是最突出的。注意，\(Z\) 也因 \(Y\) 而异常，但它只是继承了来自 \(Y\) 的高值。归因方法能够识别这一点，并区分 \(Y\) 和 \(Z\) 的贡献。如果是负贡献，相应的节点甚至会降低异常的可能性，即减少其表观严重程度。

关于分数的详细解释，请参阅引用的论文。以下部分也提供了一些直观理解。

理解该方法#

在此方法中，我们使用可逆因果机制来重建和修改导致特定观测的噪声。然后我们问：“如果特定节点的噪声值来自其‘正常’分布，我们是否仍然会在目标节点中观测到异常值？”。根据上游噪声变量的已知分布改变其值后，目标节点中异常严重程度的变化，表明该节点对异常的贡献。使用噪声值而非实际节点值的优势在于，我们只测量源自该节点的影响，而不是继承自其父节点的影响。

该过程可以概括为

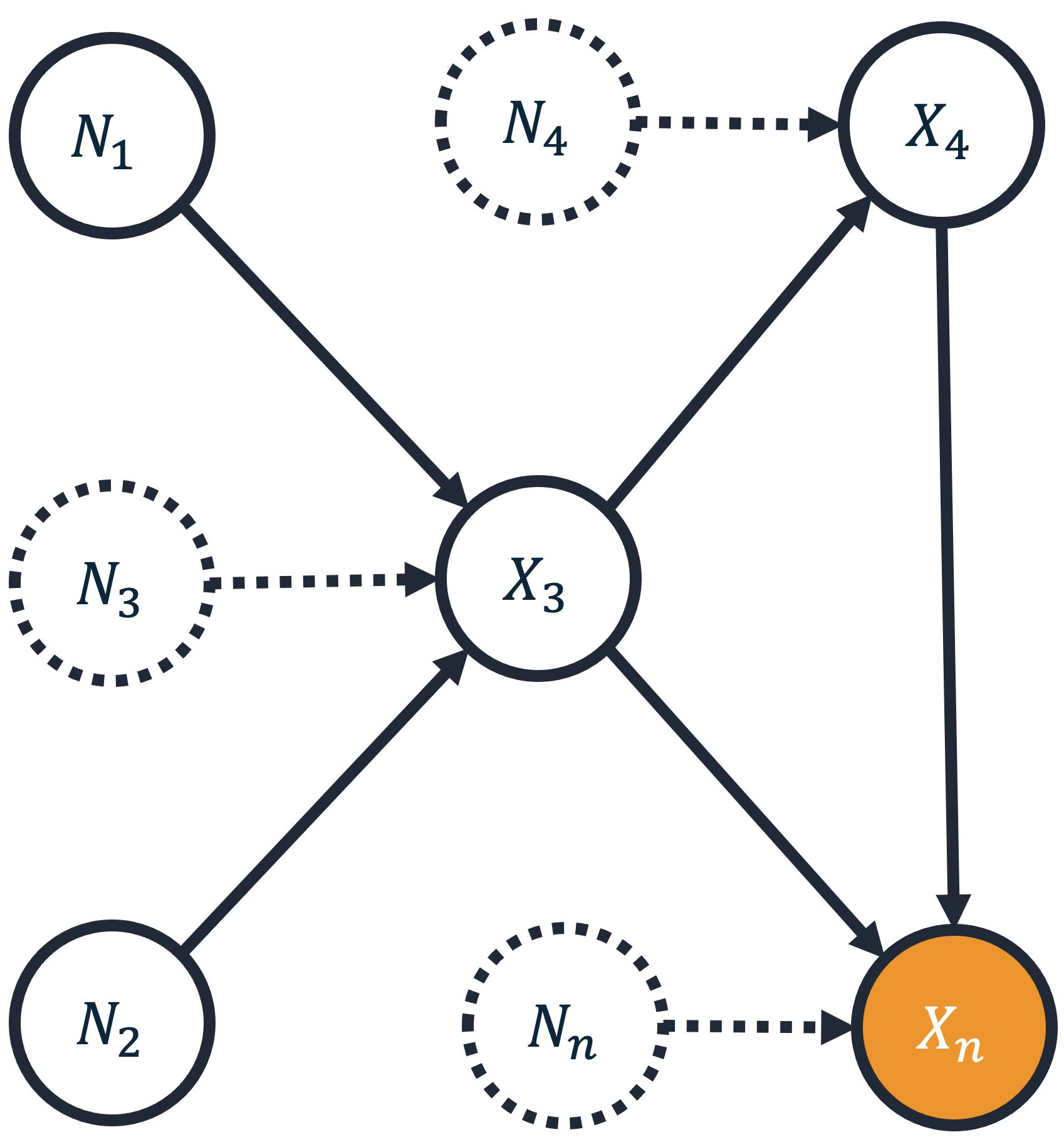
../../../_images/attribute_anomalies.png

将目标变量 \(X_n\) 的异常分数定义为 \(S(x_n) := -log P(g(X_n) \geq g(x_n))\)，其中 \(g\) 为某个特征映射。此处，\(g\) 是任意异常评分器，例如隔离森林、中位数/均值差或任何其他给出异常分数的模型。观测 \(x_n\) 的信息论分数 \(S(x_n)\) 随后是尺度不变的，并且独立于异常评分器的选择。
将节点 \(j\) 的贡献定义为 \(log \frac{P(g(X_n) \geq g(x_n) | \text{用随机值替换所有噪声值 } n_1, ..., n_{j-1})}{P(g(X_n) \geq g(x_n) | \text{用随机值替换所有噪声值 } n_1, ..., n_j)}\)，其中“随机值”是相对于学到的噪声分布。此对数比衡量随机化噪声 \(N_j\) 如何降低异常事件的可能性。
对所有排序下的贡献进行对称化，以消除节点重新排序带来的歧义。我们为此使用 Shapley 对称化。
最终的 Shapley 值之和等于异常分数 \(S(x_n)\)。

这种方法的关键特性是只有罕见事件才能获得高贡献；常见事件无法解释罕见事件。

简单示例：一个基本且直接的例子，我们可以直接获得贡献，即当我们有两个骰子时，一个有四面，另一个有 100 面（例如，来自龙与地下城游戏）。如果我们掷骰子并得到 (1, 1)，则此事件的“异常”分数是 \(log(4 \cdot 100) = log(4) + log(100)\)。在这里，每个骰子对此事件的贡献直接基于总和；四面骰子贡献了 23%，而 100 面骰子对 (1, 1) 事件贡献了 77%。

异常归因#

如何使用#

相关示例 Notebook#

理解该方法#