直接效应：量化箭头强度#

通过量化箭头的强度，我们回答以下问题：

原因对其直接效应的因果影响有多强？

文献中有多种衡量因果影响的定义，而 DoWhy 提供了一种实现，用于衡量父节点对其子节点的直接影响，忽略通过其他节点路径产生的间接影响。此方法基于以下论文：

Dominik Janzing, David Balduzzi, Moritz Grosse-Wentrup, Bernhard Schölkopf. 量化因果影响 The Annals of Statistics, Vol. 41, No. 5, 2324-2358, 2013.

如何使用#

为了演示如何使用该方法，让我们生成一些数据。

>>> import numpy as np, pandas as pd, networkx as nx
>>> from dowhy import gcm
>>> np.random.seed(10)  # to reproduce these results

>>> Z = np.random.normal(loc=0, scale=1, size=1000)
>>> X = 2*Z + np.random.normal(loc=0, scale=1, size=1000)
>>> Y = 3*X + 4*Z + np.random.normal(loc=0, scale=1, size=1000)
>>> data = pd.DataFrame(dict(X=X, Y=Y, Z=Z))

接下来，我们将使用 DoWhy 的 GCM 框架将因果关系建模为概率因果模型，并将其拟合到数据。

>>> causal_model = gcm.ProbabilisticCausalModel(nx.DiGraph([('Z', 'Y'), ('Z', 'X'), ('X', 'Y')]))
>>> gcm.auto.assign_causal_mechanisms(causal_model, data)
>>> gcm.fit(causal_model, data)

最后，我们可以估计指向目标节点（例如 \(Y\)）的传入箭头的强度。

>>> strength = gcm.arrow_strength(causal_model, 'Y')
>>> strength
    {('X', 'Y'): 41.321925893102716,
     ('Z', 'Y'): 14.736197949517237}

结果解释： 默认情况下，对于连续实值目标，箭头强度的标量值测量单位是方差；对于分类目标，测量单位是比特数（即 KL 散度）。上文中，我们观察到从 \(X\) 到 \(Y\) 的直接影响（约 41.32）比从 \(Z\) 到 \(Y\) 的直接影响（约 14.73）强（约 2.7 倍）。粗略地说，“移除”从 \(X\) 到 \(Y\) 的箭头会使 \(Y\) 的方差增加约 41.32 个单位，而移除 \(Z \to Y\) 会使 \(Y\) 的方差增加约 14.73 个单位。

在理解该方法章节中，我们解释了“移除”边的含义。特别是，我们简要解释了我们量化箭头强度方法背后的科学原理。

理解该方法#

我们将使用下面的因果图来说明该方法背后的核心思想。

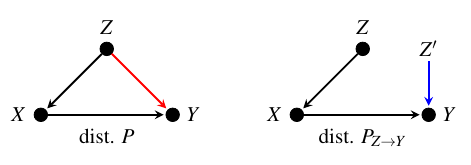
这里，我们想测量从节点 \(Z\) 到节点 \(Y\) 的箭头强度，同时忽略通过 \(X\) 的任何间接效应。为此，首先回想一下，我们可以通过每个变量在其父节点条件下的条件分布的乘积，从因果图中获得变量的联合分布 \(P\)。

然后，我们通过切断从 \(Z\) 到 \(Y\) 的边，并使用 \(Z\) 的独立同分布副本（图中表示为 \(Z'\)）作为 \(Y\) 的输入，来创建一个新的联合分布 \(P_{Z \to Y}\)。实际中可以通过随机打乱观察到的 \(Z\) 值来模拟 \(Z'\) 的分布。从 \(Z\) 到 \(Y\) 的箭头强度，表示为 \(C_{Z \to Y}\)，然后计算为切断后的分布:math:P_{Z to Y} 与原始联合分布 \(P\) 之间的距离。

\[C_{Z \to Y} := D(P\; || P_{Z \to Y})\]

用于计算箭头强度的距离度量 \(D\) 可以是任何合适的度量，例如方差之差或 KL 散度。默认情况下，库会根据数据类型使用特定的度量，但这可以根据用例进行完全自定义。

注意，在切断边时，原始联合分布与切断后联合分布之间，只有目标变量的因果机制发生变化。因此，目标边际分布的任何变化都归因于目标因果机制的变化。这使我们能够通过移除边时目标边际分布属性（例如，方差）的变化来量化箭头强度。

自定义距离度量#

默认情况下，arrow_strength 对于连续实值目标使用方差之差来衡量箭头强度，对于分类目标则使用 KL 散度。但是，我们也可以使用 difference_estimation_func 参数传入我们自己的度量选择。例如，要以均值的变化来衡量箭头强度，我们可以定义

>>> def mean_diff(Y_old, Y_new): return np.mean(Y_new) - np.mean(Y_old)

然后估计箭头强度

>>> gcm.arrow_strength(causal_model, 'Y', difference_estimation_func=mean_diff)
    {('X', 'Y'): 0.11898914602350251,
     ('Z', 'Y'): 0.07811542095834415}

这里的小结果是预期的；在我们的例子中，无论是否移除传入的箭头，\(Y\) 的均值都保持为 \(0\)。因此，传入 \(Y\) 的箭头对其均值的影响应微不足道。

总而言之，箭头强度可以用不同的单位衡量（例如，均值、方差、比特）。因此，我们建议用户根据数据和解释选择有意义的单位，以便在实践中应用此方法。

直接效应：量化箭头强度#

如何使用#

相关示例 Notebook#

理解该方法#

自定义距离度量#