使用 DoWhy 和 EconML 计算条件平均治疗效果 (CATE)#
这是一项实验性功能,我们在其中使用 DoWhy 中的 EconML 方法。使用 EconML 可以通过不同方法进行 CATE 估计。
DoWhy 中因果推断的所有四个步骤保持不变:建模、识别、估计和反驳。主要区别在于我们现在在估计步骤中调用 econml 方法。还有一个使用线性回归的简单示例,以帮助理解 CATE 估计器背后的直觉。
所有数据集均使用线性结构方程生成。
[1]:
%load_ext autoreload
%autoreload 2
[2]:
import numpy as np
import pandas as pd
import logging
import dowhy
from dowhy import CausalModel
import dowhy.datasets
import econml
import warnings
warnings.filterwarnings('ignore')
BETA = 10
[3]:
data = dowhy.datasets.linear_dataset(BETA, num_common_causes=4, num_samples=10000,
num_instruments=2, num_effect_modifiers=2,
num_treatments=1,
treatment_is_binary=False,
num_discrete_common_causes=2,
num_discrete_effect_modifiers=0,
one_hot_encode=False)
df=data['df']
print(df.head())
print("True causal estimate is", data["ate"])
X0 X1 Z0 Z1 W0 W1 W2 W3 v0 \
0 -0.520835 0.756229 0.0 0.547725 -0.348991 -0.917974 0 3 14.006824
1 -1.560984 0.546710 0.0 0.474327 -0.652985 -1.886253 0 2 5.116915
2 -0.631737 0.866077 0.0 0.993189 -0.317968 0.702546 2 2 20.962792
3 -1.471904 0.208802 1.0 0.543871 -1.858522 -2.549787 0 2 9.131259
4 -2.163623 1.074842 1.0 0.522107 -0.281958 0.102664 1 2 24.442475
y
0 181.573850
1 56.379803
2 274.811687
3 80.831273
4 301.137661
True causal estimate is 11.573149205663968
[4]:
model = CausalModel(data=data["df"],
treatment=data["treatment_name"], outcome=data["outcome_name"],
graph=data["gml_graph"])
[5]:
model.view_model()
from IPython.display import Image, display
display(Image(filename="causal_model.png"))
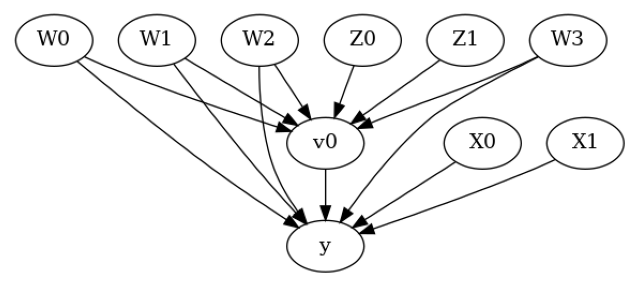
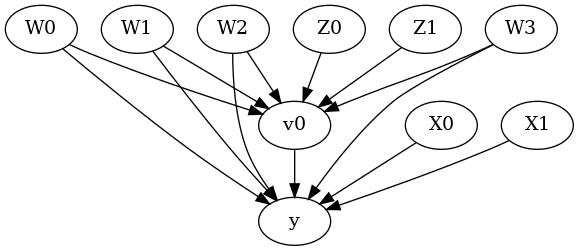
[6]:
identified_estimand= model.identify_effect(proceed_when_unidentifiable=True)
print(identified_estimand)
Estimand type: EstimandType.NONPARAMETRIC_ATE
### Estimand : 1
Estimand name: backdoor
Estimand expression:
d
─────(E[y|W3,W2,W1,W0])
d[v₀]
Estimand assumption 1, Unconfoundedness: If U→{v0} and U→y then P(y|v0,W3,W2,W1,W0,U) = P(y|v0,W3,W2,W1,W0)
### Estimand : 2
Estimand name: iv
Estimand expression:
⎡ -1⎤
⎢ d ⎛ d ⎞ ⎥
E⎢─────────(y)⋅⎜─────────([v₀])⎟ ⎥
⎣d[Z₀ Z₁] ⎝d[Z₀ Z₁] ⎠ ⎦
Estimand assumption 1, As-if-random: If U→→y then ¬(U →→{Z0,Z1})
Estimand assumption 2, Exclusion: If we remove {Z0,Z1}→{v0}, then ¬({Z0,Z1}→y)
### Estimand : 3
Estimand name: frontdoor
No such variable(s) found!
线性模型#
首先,让我们使用线性模型建立一些估计 CATE 的直觉。效应调节器(导致异质治疗效果)可以建模为与治疗的交互项。因此,它们的值调节治疗的效果。
下面是治疗从 0 变为 1 的估计效果。
[7]:
linear_estimate = model.estimate_effect(identified_estimand,
method_name="backdoor.linear_regression",
control_value=0,
treatment_value=1)
print(linear_estimate)
*** Causal Estimate ***
## Identified estimand
Estimand type: EstimandType.NONPARAMETRIC_ATE
### Estimand : 1
Estimand name: backdoor
Estimand expression:
d
─────(E[y|W3,W2,W1,W0])
d[v₀]
Estimand assumption 1, Unconfoundedness: If U→{v0} and U→y then P(y|v0,W3,W2,W1,W0,U) = P(y|v0,W3,W2,W1,W0)
## Realized estimand
b: y~v0+W3+W2+W1+W0+v0*X0+v0*X1
Target units:
## Estimate
Mean value: 11.573167881816286
### Conditional Estimates
__categorical__X0 __categorical__X1
(-4.375, -1.64] (-3.165, -0.208] 5.078562
(-0.208, 0.387] 8.485901
(0.387, 0.892] 10.316470
(0.892, 1.479] 12.246467
(1.479, 4.369] 15.190344
(-1.64, -1.05] (-3.165, -0.208] 6.211164
(-0.208, 0.387] 9.229992
(0.387, 0.892] 11.081200
(0.892, 1.479] 13.054074
(1.479, 4.369] 16.098330
(-1.05, -0.546] (-3.165, -0.208] 6.672065
(-0.208, 0.387] 9.717292
(0.387, 0.892] 11.599016
(0.892, 1.479] 13.509362
(1.479, 4.369] 16.612933
(-0.546, 0.0363] (-3.165, -0.208] 6.791592
(-0.208, 0.387] 10.133414
(0.387, 0.892] 12.047274
(0.892, 1.479] 13.993364
(1.479, 4.369] 17.081919
(0.0363, 2.709] (-3.165, -0.208] 7.808295
(-0.208, 0.387] 10.903614
(0.387, 0.892] 12.788630
(0.892, 1.479] 14.663872
(1.479, 4.369] 18.027674
dtype: float64
EconML 方法#
现在我们转向 EconML 包中更高级的方法来估计 CATE。
首先,让我们看看双重机器学习估计器。Method_name 对应于我们要使用的类的完全限定名称。对于双重 ML,它是“econml.dml.DML”。
目标单位定义了计算因果估计的单位。这可以是应用于原始数据框的 lambda 函数过滤器、新的 Pandas 数据框,或者对应于三种主要目标单位(“ate”、“att”和“atc”)的字符串。下面我们展示一个 lambda 函数的示例。
Method_params 直接传递给 EconML。有关允许参数的详细信息,请参阅 EconML 文档。
[8]:
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LassoCV
from sklearn.ensemble import GradientBoostingRegressor
dml_estimate = model.estimate_effect(identified_estimand, method_name="backdoor.econml.dml.DML",
control_value = 0,
treatment_value = 1,
target_units = lambda df: df["X0"]>1, # condition used for CATE
confidence_intervals=False,
method_params={"init_params":{'model_y':GradientBoostingRegressor(),
'model_t': GradientBoostingRegressor(),
"model_final":LassoCV(fit_intercept=False),
'featurizer':PolynomialFeatures(degree=1, include_bias=False)},
"fit_params":{}})
print(dml_estimate)
*** Causal Estimate ***
## Identified estimand
Estimand type: EstimandType.NONPARAMETRIC_ATE
### Estimand : 1
Estimand name: backdoor
Estimand expression:
d
─────(E[y|W3,W2,W1,W0])
d[v₀]
Estimand assumption 1, Unconfoundedness: If U→{v0} and U→y then P(y|v0,W3,W2,W1,W0,U) = P(y|v0,W3,W2,W1,W0)
## Realized estimand
b: y~v0+W3+W2+W1+W0 | X0,X1
Target units: Data subset defined by a function
## Estimate
Mean value: 13.416786686392697
Effect estimates: [[20.5674886 ]
[16.81810804]
[ 4.41081626]
[12.7590796 ]
[18.66045567]
[18.51674086]
[17.1438172 ]
[16.72935127]
[12.3084639 ]
[10.89723545]
[12.2995654 ]
[15.4393769 ]
[15.12603867]
[ 9.92507887]
[21.45669981]
[14.24272826]
[ 5.1408623 ]
[13.95199732]
[16.10403499]
[15.51334418]
[12.86616718]
[17.69517585]
[14.98275821]
[14.02400959]
[ 8.04652404]
[ 7.40925404]
[11.66325528]
[16.73155822]
[11.41878005]
[14.39183237]
[ 7.78196165]
[18.5219238 ]
[ 5.40617633]
[17.47738011]
[13.03976874]
[21.62362646]
[12.7727103 ]
[10.89263293]
[17.30916227]
[13.97571332]
[10.90617174]
[10.42957745]
[ 8.22825142]
[16.43221157]
[12.23764192]
[12.68420247]
[11.39128513]
[16.09066681]
[10.02702876]
[ 7.58134396]
[12.19220932]
[10.59733045]
[13.37447019]
[13.64565928]
[19.16869052]
[11.69113092]
[17.50618788]
[19.21822674]
[13.83940523]
[14.61733979]
[11.6829634 ]
[13.74655525]
[14.36207116]
[12.77088996]
[ 9.01665902]
[11.30305241]
[15.89790646]
[11.78357804]
[16.56510634]
[14.5326168 ]
[ 6.39768296]
[13.43185146]
[12.01891169]
[11.60103112]
[15.70616691]
[10.93777069]
[12.58731849]
[ 9.65958592]
[17.27134558]
[10.11003355]
[12.69721151]
[14.08728187]
[13.07706806]
[13.16812878]
[13.81273431]
[10.85485827]
[11.22442377]
[11.26772553]
[10.91163199]
[18.91911392]
[14.16473814]
[12.43741423]
[10.90886278]
[15.94262812]
[ 7.34136344]
[13.96326514]
[19.49004536]
[13.39017623]
[11.01312687]
[12.04871674]
[ 8.74582241]
[ 9.18646732]
[14.41435661]
[ 7.65377335]
[12.70753593]
[ 6.5546823 ]
[20.89621188]
[13.6687491 ]
[12.29115227]
[ 8.23148509]
[13.14348103]
[ 8.59881967]
[14.45936563]
[12.93855552]
[14.96923772]
[15.20999455]
[ 9.25666362]
[15.44556932]
[16.30677664]
[ 6.79309506]
[11.0248835 ]
[11.38621917]
[12.40392566]
[15.15631617]
[15.47750929]
[13.09407579]
[21.09243156]
[14.20065511]
[18.44004907]
[17.46505872]
[13.12384027]
[10.80277671]
[12.90042107]
[10.60835352]
[15.78490693]
[12.61665204]
[10.55847388]
[17.02018018]
[ 8.91050269]
[16.86815955]
[17.44050478]
[ 9.96930217]
[17.72905667]
[ 9.60855556]
[12.93686361]
[12.69410935]
[13.12214551]
[10.4047489 ]
[13.70034905]
[16.2873264 ]
[12.54950062]
[13.07973091]
[12.94038306]
[ 8.55823341]
[14.97447905]
[12.30526785]
[ 9.7865365 ]
[10.0164226 ]
[ 8.39509301]
[13.73544153]
[ 6.24179927]
[12.11277178]
[15.53916016]
[11.05322366]
[12.12149138]
[10.06573177]
[11.90917829]
[12.56205525]
[12.90046028]
[ 9.62295253]
[18.13306695]
[17.18491478]
[15.42384531]
[11.79491557]
[14.98991145]
[15.03724975]
[11.26121636]
[12.67032938]
[ 8.68729779]
[ 7.51402856]
[ 9.75685123]
[12.60398272]
[12.99152973]
[15.09644118]
[16.60299135]
[16.09588776]
[ 3.64772799]
[12.84148723]
[18.65626365]
[14.39374335]
[13.30649259]
[13.67661457]
[10.50907391]
[ 7.14469413]
[ 9.56842616]
[ 9.42719284]
[19.63900172]
[12.89246116]
[ 8.51291399]
[13.26315487]
[ 9.42047433]
[11.55964207]
[11.37217564]
[ 7.86415732]
[16.99067817]
[ 9.95581975]
[ 7.62928437]
[15.67276703]
[15.23104827]
[14.74048851]
[11.4638321 ]
[14.36781003]
[18.24133044]
[14.53730603]
[ 8.93658313]
[17.13530402]
[ 9.63114204]
[14.82085309]
[14.30631252]
[13.27430389]
[22.7958537 ]
[14.52528945]
[12.01047948]
[17.07857452]
[12.87676195]
[13.19365817]
[11.78923515]
[13.84325536]
[15.28329488]
[14.8810602 ]
[19.02864126]
[13.24922779]
[11.08788091]
[ 9.14628163]
[12.45375332]
[13.11554873]
[16.94156874]
[15.2703654 ]
[15.4388345 ]
[12.66600935]
[12.21227572]
[18.48199464]
[15.73234323]
[14.98888595]
[10.50379867]
[15.36877202]
[14.41978644]
[19.1282748 ]
[ 8.74649804]
[18.0238775 ]
[16.50881595]
[10.51615594]
[ 5.16953339]
[20.92100312]
[12.17479305]
[14.34722732]
[ 9.48866414]
[ 9.27444633]
[15.30851141]
[15.60089383]
[14.87701042]
[11.39777685]
[10.39819466]
[10.52082995]
[12.78910962]
[13.08950908]
[15.14449594]
[14.14229255]
[17.33829309]
[15.11863113]
[13.36840657]
[17.27580312]
[ 9.63258133]
[13.81493757]
[15.31935159]
[16.65902264]
[18.30038777]
[10.05234907]
[15.99178775]
[14.50080589]
[19.2293583 ]
[15.80951257]
[10.53998897]
[12.94333869]
[ 9.27430062]
[ 7.90520875]
[ 5.00443678]
[ 8.62821179]
[13.16819391]
[17.04930048]
[14.83520756]
[11.11807073]
[17.01245274]
[15.80654 ]
[13.32692666]
[12.20093365]
[14.66867576]
[11.44647894]
[19.02857772]
[15.40038588]
[11.61615852]
[12.53974592]
[ 9.5410054 ]
[11.46179022]
[16.09647595]
[10.29908036]
[10.36165292]
[17.80286842]
[17.03426414]
[14.28988041]
[ 5.36218566]
[17.68735257]
[14.90463919]
[12.50118809]
[13.20463625]
[13.45133909]
[19.52980369]
[16.36723555]
[17.95656214]
[ 9.07603694]
[12.99942557]
[ 7.58217009]
[12.25094009]
[20.62468395]
[15.53609165]
[15.05133301]
[13.82908115]
[14.40748572]
[11.60776728]
[13.26077053]
[ 7.29519633]
[14.72728296]
[13.18829522]
[22.35169842]
[11.88613095]
[11.89403583]
[13.33237917]
[18.13117447]
[16.21136452]
[ 9.46587805]
[15.05493252]
[13.11146559]
[12.94026322]
[16.74566772]
[23.87810341]
[11.38879393]
[14.16939295]
[14.46740696]
[17.20850582]
[14.87149497]
[ 9.71447662]
[ 7.90234328]
[16.45053096]
[11.76390866]
[16.19268945]
[ 9.99966499]
[13.66432805]
[17.05656237]
[13.16772128]
[15.21632243]
[12.74924754]
[16.00549041]
[18.74638992]
[ 8.81325287]
[20.21752126]
[14.41172835]
[11.44879343]
[13.86334141]
[16.00583361]
[ 6.66165918]
[12.96753674]
[ 9.60090159]
[13.28635303]
[18.4905823 ]
[ 9.24040548]
[ 8.27216878]
[12.17418539]
[ 6.78689615]
[13.10914365]
[ 9.09830979]
[15.22533319]
[18.44379055]
[ 9.53270009]
[11.06633756]
[20.46065545]
[19.78971092]
[13.14965442]
[17.03035734]
[15.86081423]
[10.07036957]
[24.56620577]
[19.94939981]
[14.09161592]
[14.38762808]
[19.65759238]
[19.37197678]
[12.76002652]
[17.86634742]]
[9]:
print("True causal estimate is", data["ate"])
True causal estimate is 11.573149205663968
[10]:
dml_estimate = model.estimate_effect(identified_estimand, method_name="backdoor.econml.dml.DML",
control_value = 0,
treatment_value = 1,
target_units = 1, # condition used for CATE
confidence_intervals=False,
method_params={"init_params":{'model_y':GradientBoostingRegressor(),
'model_t': GradientBoostingRegressor(),
"model_final":LassoCV(fit_intercept=False),
'featurizer':PolynomialFeatures(degree=1, include_bias=True)},
"fit_params":{}})
print(dml_estimate)
*** Causal Estimate ***
## Identified estimand
Estimand type: EstimandType.NONPARAMETRIC_ATE
### Estimand : 1
Estimand name: backdoor
Estimand expression:
d
─────(E[y|W3,W2,W1,W0])
d[v₀]
Estimand assumption 1, Unconfoundedness: If U→{v0} and U→y then P(y|v0,W3,W2,W1,W0,U) = P(y|v0,W3,W2,W1,W0)
## Realized estimand
b: y~v0+W3+W2+W1+W0 | X0,X1
Target units:
## Estimate
Mean value: 11.545193396441825
Effect estimates: [[12.21983071]
[10.53410266]
[12.50857838]
...
[12.10591118]
[11.42940987]
[18.22728622]]
CATE 对象和置信区间#
EconML 提供了计算置信区间的自身方法。下面示例中使用了 BootstrapInference。
[11]:
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LassoCV
from sklearn.ensemble import GradientBoostingRegressor
from econml.inference import BootstrapInference
dml_estimate = model.estimate_effect(identified_estimand,
method_name="backdoor.econml.dml.DML",
target_units = "ate",
confidence_intervals=True,
method_params={"init_params":{'model_y':GradientBoostingRegressor(),
'model_t': GradientBoostingRegressor(),
"model_final": LassoCV(fit_intercept=False),
'featurizer':PolynomialFeatures(degree=1, include_bias=True)},
"fit_params":{
'inference': BootstrapInference(n_bootstrap_samples=100, n_jobs=-1),
}
})
print(dml_estimate)
*** Causal Estimate ***
## Identified estimand
Estimand type: EstimandType.NONPARAMETRIC_ATE
### Estimand : 1
Estimand name: backdoor
Estimand expression:
d
─────(E[y|W3,W2,W1,W0])
d[v₀]
Estimand assumption 1, Unconfoundedness: If U→{v0} and U→y then P(y|v0,W3,W2,W1,W0,U) = P(y|v0,W3,W2,W1,W0)
## Realized estimand
b: y~v0+W3+W2+W1+W0 | X0,X1
Target units: ate
## Estimate
Mean value: 11.527529711637378
Effect estimates: [[12.19093781]
[10.55565123]
[12.48968174]
...
[12.1142495 ]
[11.50570656]
[18.37636746]]
95.0% confidence interval: [[[12.21716494 10.56284631 12.52228849 ... 12.14895059 11.5008028
18.41722706]]
[[12.3653399 10.68942253 12.67145822 ... 12.27769598 11.69965469
18.82137994]]]
可以提供新输入作为目标单位并对其进行 CATE 估计。#
[12]:
test_cols= data['effect_modifier_names'] # only need effect modifiers' values
test_arr = [np.random.uniform(0,1, 10) for _ in range(len(test_cols))] # all variables are sampled uniformly, sample of 10
test_df = pd.DataFrame(np.array(test_arr).transpose(), columns=test_cols)
dml_estimate = model.estimate_effect(identified_estimand,
method_name="backdoor.econml.dml.DML",
target_units = test_df,
confidence_intervals=False,
method_params={"init_params":{'model_y':GradientBoostingRegressor(),
'model_t': GradientBoostingRegressor(),
"model_final":LassoCV(),
'featurizer':PolynomialFeatures(degree=1, include_bias=True)},
"fit_params":{}
})
print(dml_estimate.cate_estimates)
[[13.58279001]
[10.41890505]
[11.24343158]
[13.72711318]
[13.35554588]
[13.62401139]
[11.78798609]
[13.37448703]
[10.96215956]
[10.33472942]]
也可以检索原始 EconML 估计器对象以进行任何进一步操作#
[13]:
print(dml_estimate._estimator_object)
<econml.dml.dml.DML object at 0x7fa48296b910>
适用于任何 EconML 方法#
除了双重机器学习,下面我们示例分析了使用正交森林、DRLearner(待修复错误)和基于神经网络的工具变量。
二元治疗,二元结果#
[14]:
data_binary = dowhy.datasets.linear_dataset(BETA, num_common_causes=4, num_samples=10000,
num_instruments=1, num_effect_modifiers=2,
treatment_is_binary=True, outcome_is_binary=True)
# convert boolean values to {0,1} numeric
data_binary['df'].v0 = data_binary['df'].v0.astype(int)
data_binary['df'].y = data_binary['df'].y.astype(int)
print(data_binary['df'])
model_binary = CausalModel(data=data_binary["df"],
treatment=data_binary["treatment_name"], outcome=data_binary["outcome_name"],
graph=data_binary["gml_graph"])
identified_estimand_binary = model_binary.identify_effect(proceed_when_unidentifiable=True)
X0 X1 Z0 W0 W1 W2 W3 v0 y
0 -1.793037 -1.399146 1.0 1.918945 -1.837178 0.236404 0.374686 1 1
1 -0.333448 0.655739 1.0 1.879264 -0.963963 -0.836016 -1.358999 1 1
2 0.888209 -0.468418 0.0 -0.009608 -2.166280 -2.133876 -0.399757 0 0
3 0.047108 -0.112075 1.0 -0.157878 0.960046 -1.215147 -1.075899 1 1
4 -1.136697 0.346339 0.0 1.288702 1.054372 1.008400 -0.854865 1 1
... ... ... ... ... ... ... ... .. ..
9995 -0.335132 0.656147 1.0 1.728914 0.080934 -0.744671 -2.788066 1 1
9996 0.722839 -0.265596 1.0 0.752381 0.256524 1.775311 -1.318501 1 1
9997 -0.297344 -0.506091 0.0 2.640441 -1.229769 -0.645940 -0.184254 1 1
9998 1.975701 -0.538139 1.0 1.343029 -2.131004 0.019488 -0.951944 1 1
9999 -0.008991 0.438879 0.0 1.805087 -0.785812 -1.315040 -0.813219 1 1
[10000 rows x 9 columns]
使用 DRLearner 估计器#
[15]:
from sklearn.linear_model import LogisticRegressionCV
#todo needs binary y
drlearner_estimate = model_binary.estimate_effect(identified_estimand_binary,
method_name="backdoor.econml.dr.LinearDRLearner",
confidence_intervals=False,
method_params={"init_params":{
'model_propensity': LogisticRegressionCV(cv=3, solver='lbfgs', multi_class='auto')
},
"fit_params":{}
})
print(drlearner_estimate)
print("True causal estimate is", data_binary["ate"])
*** Causal Estimate ***
## Identified estimand
Estimand type: EstimandType.NONPARAMETRIC_ATE
### Estimand : 1
Estimand name: backdoor
Estimand expression:
d
─────(E[y|W3,W2,W1,W0])
d[v₀]
Estimand assumption 1, Unconfoundedness: If U→{v0} and U→y then P(y|v0,W3,W2,W1,W0,U) = P(y|v0,W3,W2,W1,W0)
## Realized estimand
b: y~v0+W3+W2+W1+W0 | X0,X1
Target units: ate
## Estimate
Mean value: 0.5076726046276433
Effect estimates: [[0.33560034]
[0.58497292]
[0.46481803]
...
[0.45091439]
[0.46551344]
[0.56250906]]
True causal estimate is 0.3994
工具变量方法#
[16]:
dmliv_estimate = model.estimate_effect(identified_estimand,
method_name="iv.econml.iv.dml.DMLIV",
target_units = lambda df: df["X0"]>-1,
confidence_intervals=False,
method_params={"init_params":{
'discrete_treatment':False,
'discrete_instrument':False
},
"fit_params":{}})
print(dmliv_estimate)
*** Causal Estimate ***
## Identified estimand
Estimand type: EstimandType.NONPARAMETRIC_ATE
### Estimand : 1
Estimand name: iv
Estimand expression:
⎡ -1⎤
⎢ d ⎛ d ⎞ ⎥
E⎢─────────(y)⋅⎜─────────([v₀])⎟ ⎥
⎣d[Z₀ Z₁] ⎝d[Z₀ Z₁] ⎠ ⎦
Estimand assumption 1, As-if-random: If U→→y then ¬(U →→{Z0,Z1})
Estimand assumption 2, Exclusion: If we remove {Z0,Z1}→{v0}, then ¬({Z0,Z1}→y)
## Realized estimand
b: y~v0+W3+W2+W1+W0 | X0,X1
Target units: Data subset defined by a function
## Estimate
Mean value: 12.318378868817403
Effect estimates: [[12.36189086]
[12.65896699]
[ 9.27652617]
...
[11.52012298]
[12.72535513]
[11.49785524]]
Metalearners#
[17]:
data_experiment = dowhy.datasets.linear_dataset(BETA, num_common_causes=5, num_samples=10000,
num_instruments=2, num_effect_modifiers=5,
treatment_is_binary=True, outcome_is_binary=False)
# convert boolean values to {0,1} numeric
data_experiment['df'].v0 = data_experiment['df'].v0.astype(int)
print(data_experiment['df'])
model_experiment = CausalModel(data=data_experiment["df"],
treatment=data_experiment["treatment_name"], outcome=data_experiment["outcome_name"],
graph=data_experiment["gml_graph"])
identified_estimand_experiment = model_experiment.identify_effect(proceed_when_unidentifiable=True)
X0 X1 X2 X3 X4 Z0 Z1 \
0 1.173809 1.459526 -0.734409 1.271968 -1.139768 1.0 0.601753
1 0.414449 0.717820 -0.550879 1.542919 -0.061394 1.0 0.249743
2 1.482742 0.255102 -1.919030 -0.285862 -0.863307 1.0 0.756099
3 0.026937 -1.199462 -0.973142 -0.289309 -1.290227 0.0 0.136899
4 0.024090 0.561883 -1.853785 1.091348 -1.094074 0.0 0.825579
... ... ... ... ... ... ... ...
9995 2.078520 0.356694 -2.000105 0.670750 -1.748592 1.0 0.741970
9996 -0.124005 -0.166842 -0.093543 0.959838 -1.905656 0.0 0.300446
9997 1.150224 -1.330117 0.489152 0.191833 0.757605 1.0 0.193838
9998 1.304547 0.938613 0.023811 1.904848 -0.811467 1.0 0.214526
9999 0.732159 0.033379 -0.953824 1.192767 -1.144805 1.0 0.375597
W0 W1 W2 W3 W4 v0 y
0 0.136926 -0.476399 -0.570402 0.077995 -0.197060 1 4.698979
1 0.006260 2.123803 -0.660587 0.510811 0.708137 1 21.577703
2 -0.271943 -1.551507 -1.564531 -0.826516 -0.109544 1 -14.805524
3 0.118405 1.626826 -0.408900 -0.041457 -0.787333 1 7.264344
4 -1.691144 1.842948 0.261925 -1.378161 1.596990 1 11.047906
... ... ... ... ... ... .. ...
9995 1.196646 2.431578 0.756643 -0.104238 -1.087868 1 17.433346
9996 -0.753776 1.279296 0.805955 -0.917385 -1.207200 0 1.261266
9997 0.075716 0.774895 -0.733659 -0.301633 1.135854 1 17.049905
9998 2.535041 1.245978 -0.121139 -0.032694 -0.994657 1 26.679028
9999 0.484762 0.763548 -1.651844 0.680308 -2.926768 1 -4.694555
[10000 rows x 14 columns]
[18]:
from sklearn.ensemble import RandomForestRegressor
metalearner_estimate = model_experiment.estimate_effect(identified_estimand_experiment,
method_name="backdoor.econml.metalearners.TLearner",
confidence_intervals=False,
method_params={"init_params":{
'models': RandomForestRegressor()
},
"fit_params":{}
})
print(metalearner_estimate)
print("True causal estimate is", data_experiment["ate"])
*** Causal Estimate ***
## Identified estimand
Estimand type: EstimandType.NONPARAMETRIC_ATE
### Estimand : 1
Estimand name: backdoor
Estimand expression:
d
─────(E[y|W3,W2,W1,W0,W4])
d[v₀]
Estimand assumption 1, Unconfoundedness: If U→{v0} and U→y then P(y|v0,W3,W2,W1,W0,W4,U) = P(y|v0,W3,W2,W1,W0,W4)
## Realized estimand
b: y~v0+X4+X0+X3+X1+X2+W3+W2+W1+W0+W4
Target units: ate
## Estimate
Mean value: 14.846358811540133
Effect estimates: [[10.21441061]
[20.81706358]
[-1.88236367]
...
[20.25643333]
[23.70695711]
[ 4.46810009]]
True causal estimate is 8.16819957456251
避免重新训练估计器#
一旦估计器拟合完毕,就可以重复用于估计不同数据点的效果。在这种情况下,您可以将 fit_estimator=False 传递给 estimate_effect。这适用于任何 EconML 估计器。下面我们展示了 T-learner 的示例。
[19]:
# For metalearners, need to provide all the features (except treatmeant and outcome)
metalearner_estimate = model_experiment.estimate_effect(identified_estimand_experiment,
method_name="backdoor.econml.metalearners.TLearner",
confidence_intervals=False,
fit_estimator=False,
target_units=data_experiment["df"].drop(["v0","y", "Z0", "Z1"], axis=1)[9995:],
method_params={})
print(metalearner_estimate)
print("True causal estimate is", data_experiment["ate"])
*** Causal Estimate ***
## Identified estimand
Estimand type: EstimandType.NONPARAMETRIC_ATE
### Estimand : 1
Estimand name: backdoor
Estimand expression:
d
─────(E[y|W3,W2,W1,W0,W4])
d[v₀]
Estimand assumption 1, Unconfoundedness: If U→{v0} and U→y then P(y|v0,W3,W2,W1,W0,W4,U) = P(y|v0,W3,W2,W1,W0,W4)
## Realized estimand
b: y~v0+X4+X0+X3+X1+X2+W3+W2+W1+W0+W4
Target units: Data subset provided as a data frame
## Estimate
Mean value: 14.565445047253522
Effect estimates: [[12.60870682]
[11.78702789]
[20.25643333]
[23.70695711]
[ 4.46810009]]
True causal estimate is 8.16819957456251
反驳估计结果#
添加一个随机共同原因变量#
[20]:
res_random=model.refute_estimate(identified_estimand, dml_estimate, method_name="random_common_cause")
print(res_random)
Refute: Add a random common cause
Estimated effect:12.241115919202636
New effect:12.169842164671763
p value:0.02
添加一个未观测到的共同原因变量#
[21]:
res_unobserved=model.refute_estimate(identified_estimand, dml_estimate, method_name="add_unobserved_common_cause",
confounders_effect_on_treatment="linear", confounders_effect_on_outcome="linear",
effect_strength_on_treatment=0.01, effect_strength_on_outcome=0.02)
print(res_unobserved)
Refute: Add an Unobserved Common Cause
Estimated effect:12.241115919202636
New effect:12.12830320273598
将治疗替换为随机(安慰剂)变量#
[22]:
res_placebo=model.refute_estimate(identified_estimand, dml_estimate,
method_name="placebo_treatment_refuter", placebo_type="permute",
num_simulations=10 # at least 100 is good, setting to 10 for speed
)
print(res_placebo)
Refute: Use a Placebo Treatment
Estimated effect:12.241115919202636
New effect:-0.007014803477057729
p value:0.348413255039955
移除数据的随机子集#
[23]:
res_subset=model.refute_estimate(identified_estimand, dml_estimate,
method_name="data_subset_refuter", subset_fraction=0.8,
num_simulations=10)
print(res_subset)
Refute: Use a subset of data
Estimated effect:12.241115919202636
New effect:12.151513329399062
p value:0.020034500872382233
将会有更多反驳方法,特别是针对 CATE 估计器的方法。