医疗案例中的反事实分析#

在此示例中，我们研究了一个案例，其中我们希望对已经发生的事件提出反事实问题。我们重点关注一个与视力问题相关的远程医疗示例，我们知道三个观测变量的因果结构，并且希望提出基于“如果我遵循了与远程医疗应用建议不同的方法，会发生什么？”这种类型的问题。

更具体地说，我们考虑以下案例。爱丽丝经历着严重的眼干，由于她居住的地方无法去看眼科医生，她决定使用一个远程医疗在线平台。她按照步骤报告了她的病史，病史揭示了爱丽丝是否患有罕见的过敏症，平台最终向她推荐了两种可能的眼药水，成分略有不同（“选项 1”和“选项 2”）。爱丽丝在网上快速搜索了一下，发现选项 1 有很多好评。然而，她还是决定使用选项 2，因为她妈妈过去也用过，而且效果很好。几天后，爱丽丝的视力明显好转，症状开始消失。但是，她非常好奇，如果她使用了非常受欢迎的选项 1，甚至什么都没做，会发生什么。

只要用户报告了他们所选择选项的结果，平台就提供了提出反事实问题的可能性。

数据#

我们有一个包含三个观测变量的数据库：一个表示视力质量的从 0 到 1 的连续变量（“Vision”）、一个表示患者是否患有罕见病症（即过敏）的二元变量（“Condition”），以及一个可以取三个值（0：“什么都不做”，1：“选项 1”或 2：“选项 2”）的分类变量（“Treatment”）。数据如下所示

[1]:

import pandas as pd

medical_data = pd.read_csv('patients_database.csv')
medical_data.head()

[1]:
Condition Treatment Vision
0 0 2 0.111728
1 0 0 0.191516
2 0 2 0.163924
3 0 1 0.886563
4 0 1 0.761090 
[2]:

medical_data.iloc[0:100].plot(figsize=(15, 10))

[2]:

<Axes: >
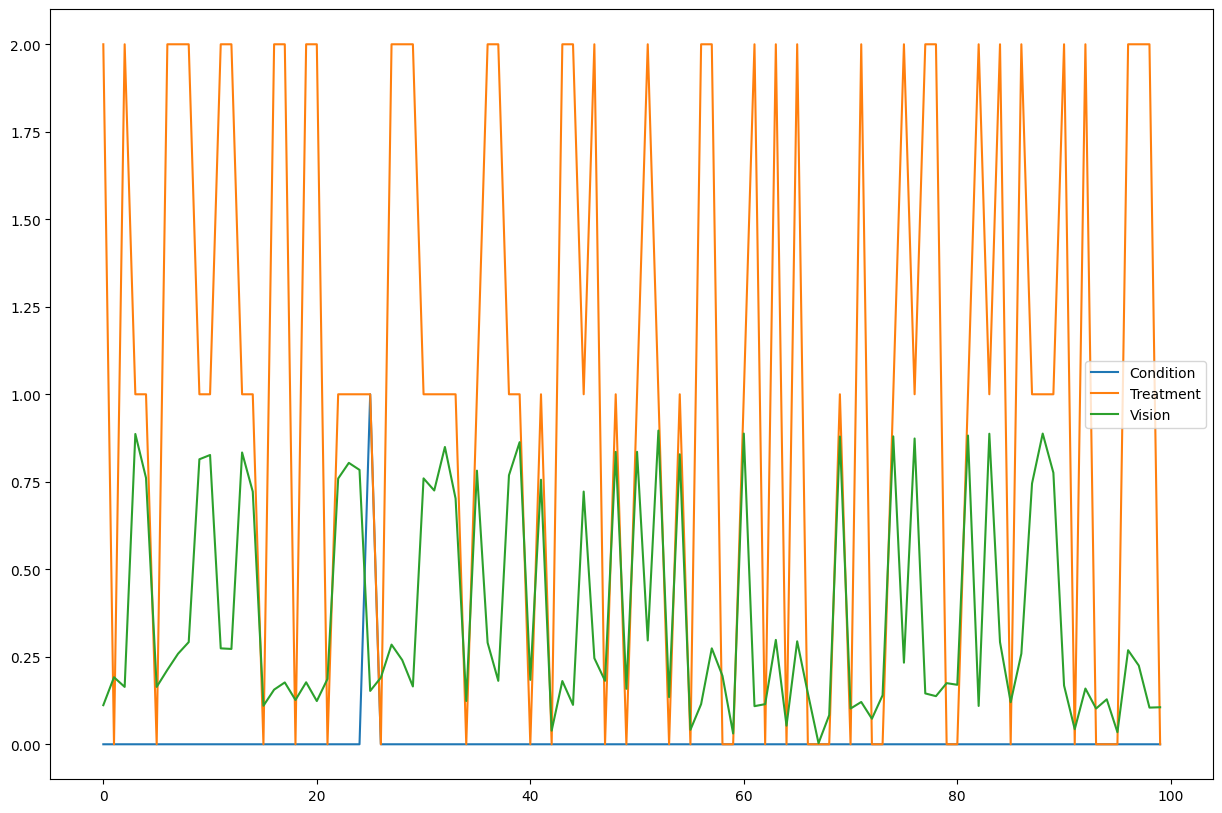
../_images/example_notebooks_gcm_counterfactual_medical_dry_eyes_4_1.png

该数据集反映了患者根据是否患有罕见 Condition 来选择三种 Treatment 选项之一后的 Vision。请注意，数据集没有关于患者治疗前原始视力（即 Vision 变量的噪声）的信息。正如我们将在下面看到的，只要我们有一个后非线性模型（例如 ANM），Vision 的这一噪声部分就可以通过反事实算法恢复。用于生成数据的结构因果模型在附录中详细解释。这三个观测节点中的每一个都有一个未被观测到的内在噪声。

图的建模#

我们知道 Treatment 节点和 Condition 节点导致 Vision，但我们不知道结构因果模型。然而，我们可以从观测数据中学习它，特别是只要后非线性模型假设不被违反，我们就能够重构特定观测的噪声。我们假设这个图正确地表示了因果关系，并且假设没有隐藏的混杂因素（因果充分性）。基于给定的图和数据，我们就可以拟合因果模型并开始回答反事实问题。

[3]:

import networkx as nx
import dowhy.gcm as gcm
from dowhy.utils import plot

causal_model = gcm.InvertibleStructuralCausalModel(nx.DiGraph([('Treatment', 'Vision'), ('Condition', 'Vision')]))
gcm.auto.assign_causal_mechanisms(causal_model, medical_data)

plot(causal_model.graph)

gcm.fit(causal_model, medical_data)
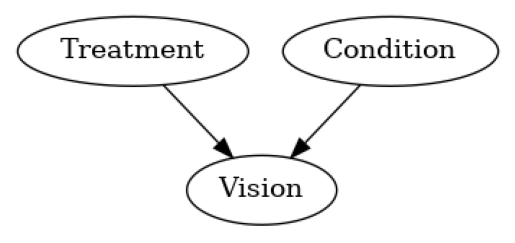
../_images/example_notebooks_gcm_counterfactual_medical_dry_eyes_7_0.png 
Fitting causal mechanism of node Condition: 100%|██████████| 3/3 [00:00<00:00, 30.13it/s]

或者，我们现在也可以评估拟合的因果模型

[4]:

print(gcm.evaluate_causal_model(causal_model, medical_data))

Evaluating causal mechanisms...: 100%|██████████| 3/3 [00:00<00:00, 3583.85it/s]
Test permutations of given graph: 100%|██████████| 6/6 [00:00<00:00, 89.40it/s]
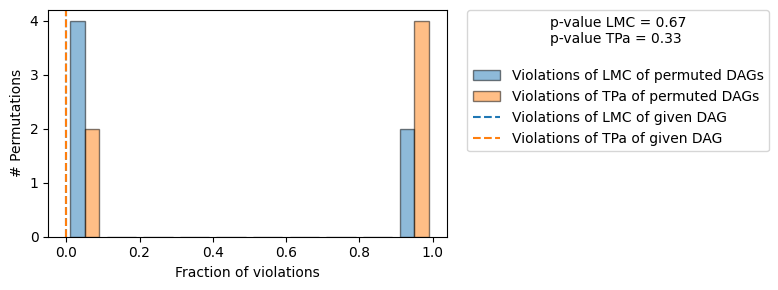
../_images/example_notebooks_gcm_counterfactual_medical_dry_eyes_9_1.png 
Evaluated the performance of the causal mechanisms and the invertibility assumption of the causal mechanisms and the overall average KL divergence between generated and observed distribution and the graph structure. The results are as follows:

==== Evaluation of Causal Mechanisms ====
The used evaluation metrics are:
- KL divergence (only for root-nodes): Evaluates the divergence between the generated and the observed distribution.
- Mean Squared Error (MSE): Evaluates the average squared differences between the observed values and the conditional expectation of the causal mechanisms.
- Normalized MSE (NMSE): The MSE normalized by the standard deviation for better comparison.
- R2 coefficient: Indicates how much variance is explained by the conditional expectations of the mechanisms. Note, however, that this can be misleading for nonlinear relationships.
- F1 score (only for categorical non-root nodes): The harmonic mean of the precision and recall indicating the goodness of the underlying classifier model.
- (normalized) Continuous Ranked Probability Score (CRPS): The CRPS generalizes the Mean Absolute Percentage Error to probabilistic predictions. This gives insights into the accuracy and calibration of the causal mechanisms.
NOTE: Every metric focuses on different aspects and they might not consistently indicate a good or bad performance.
We will mostly utilize the CRPS for comparing and interpreting the performance of the mechanisms, since this captures the most important properties for the causal model.

--- Node Treatment
- The KL divergence between generated and observed distribution is 0.0.
The estimated KL divergence indicates an overall very good representation of the data distribution.

--- Node Condition
- The KL divergence between generated and observed distribution is 0.0.
The estimated KL divergence indicates an overall very good representation of the data distribution.

--- Node Vision
- The MSE is 0.003263619495320028.
- The NMSE is 0.1825934384257641.
- The R2 coefficient is 0.9666581502186975.
- The normalized CRPS is 0.10654769436589524.
The estimated CRPS indicates a very good model performance.

==== Evaluation of Invertible Functional Causal Model Assumption ====

--- The model assumption for node Vision is not rejected with a p-value of 0.3758057876871662 (after potential adjustment) and a significance level of 0.05.
This implies that the model assumption might be valid.

Note that these results are based on statistical independence tests, and the fact that the assumption was not rejected does not necessarily imply that it is correct. There is just no evidence against it.

==== Evaluation of Generated Distribution ====
The overall average KL divergence between the generated and observed distribution is 0.0
The estimated KL divergence indicates an overall very good representation of the data distribution.

==== Evaluation of the Causal Graph Structure ====
+-------------------------------------------------------------------------------------------------------+
|                                         Falsification Summary                                         |
+-------------------------------------------------------------------------------------------------------+
| The given DAG is not informative because 2 / 6 of the permutations lie in the Markov                  |
| equivalence class of the given DAG (p-value: 0.33).                                                   |
| The given DAG violates 0/2 LMCs and is better than 33.3% of the permuted DAGs (p-value: 0.67).        |
| Based on the provided significance level (0.2) and because the DAG is not informative,                |
| we do not reject the DAG.                                                                             |
+-------------------------------------------------------------------------------------------------------+

==== NOTE ====
Always double check the made model assumptions with respect to the graph structure and choice of causal mechanisms.
All these evaluations give some insight into the goodness of the causal model, but should not be overinterpreted, since some causal relationships can be intrinsically hard to model. Furthermore, many algorithms are fairly robust against misspecifications or poor performances of causal mechanisms.

这证实了我们因果模型的准确性。

现在回到我们的原始问题，加载爱丽丝的数据，她恰好患有罕见过敏症 (Condition = 1)。

[5]:

specific_patient_data = pd.read_csv('newly_come_patients.csv')
specific_patient_data.head()

[5]:
Condition Treatment Vision
0 1 2 0.883874

回答爱丽丝的反事实查询#

在希望检查如果事件没有发生或发生方式不同时的假设结果的案例中，我们采用基于结构因果模型的所谓反事实逻辑。已知：- 我们知道爱丽丝的治疗是选项 2。- 爱丽丝患有罕见过敏症 (Condition=1)。- 治疗选项 2 后，爱丽丝的视力为 0.78 (Vision=0.78)。- 我们能够根据学习到的结构因果模型恢复噪声。

我们现在可以检查如果 Treatment 节点不同，她的 Vision 的反事实结果。在下面，我们看看如果爱丽丝没有接受任何治疗 (Treatment=0) 以及如果她接受了其他眼药水 (Treatment=1) 时，她的 Vision 的反事实值。

[6]:

counterfactual_data1 = gcm.counterfactual_samples(causal_model,
                                                  {'Treatment': lambda x: 1},
                                                  observed_data = specific_patient_data)

counterfactual_data2 = gcm.counterfactual_samples(causal_model,
                                                  {'Treatment': lambda x: 0},
                                                  observed_data = specific_patient_data)


import matplotlib.pyplot as plt

df_plot2 = pd.DataFrame()
df_plot2['Vision after option 2'] = specific_patient_data['Vision']
df_plot2['Counterfactual vision (option 1)'] = counterfactual_data1['Vision']
df_plot2['Counterfactual vision (No treatment)'] = counterfactual_data2['Vision']

df_plot2.plot.bar(title="Counterfactual outputs")
plt.xlabel('Alice')
plt.ylabel('Eyesight quality')
plt.legend()

[6]:

<matplotlib.legend.Legend at 0x7fc783d740a0>
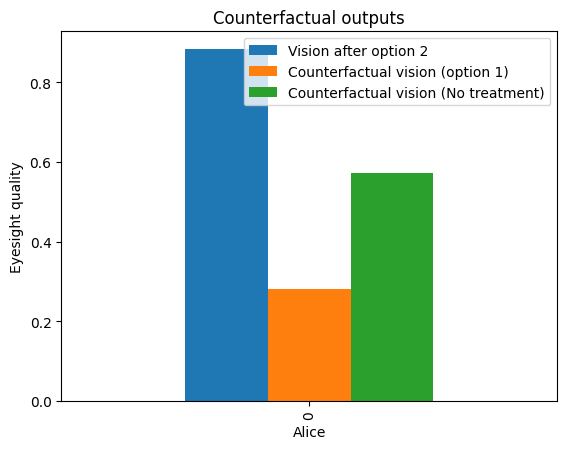
../_images/example_notebooks_gcm_counterfactual_medical_dry_eyes_14_1.png

我们在这里看到的是，如果爱丽丝选择了选项 1，她的 Vision 会比选项 2 更差。因此，她意识到她在病史中报告的罕见病症 (Condition=1) 可能是导致对受欢迎的选项 1 产生过敏反应的原因。爱丽丝也能够看到，如果她没有接受任何推荐选项，她的视力会比她选择的选项 2 更差（变量 Vision 的相对值更小）。

附录：远程医疗应用内部使用的内容。患者日志的数据生成#

这里我们描述了加性噪声模型的 SCM \(f_{p1, p2}\)：\(Vision = N_V + f_{p1, p2}(Treatment, Condition)\)。我们对三个观测变量 \(N_T, N_C\) 和 \(N_V\) 的内在加性噪声进行采样。目标变量 Vision 是加性噪声 \(N_V\) 加上其输入节点函数，如下所述。

\(Treatment = N_T\) ~ 0, 1 或 2，概率分别为 33%：33% 的用户什么都不做，33% 选择选项 1，33% 选择选项 2。这与患者是否患有罕见病症无关。

\(Condition = N_C\) ~ Bernoulli(0.01)：患者是否患有罕见病症

$Vision = N_V + f_{p1, p2}(Treatment, Condition) = N_V - P_1(1 - Condition)(1-Treatment)(2-Treatment) + 2P_2(1-Condition)Treatment(2-Treatment) + P_2(1-Condition)(3-Treatment)(1-Treatment)Treatment - 2P_2 Condition Treatment(2-Treatment) - P_2 Condition(3-Treatment)(1-Treatment)Treatment $ 患者的视力，其中

\(P_1\) 是一个常数，如果患者没有罕见病症且未服用任何药物，其原始视力将因此降低。

\(P_2\) 是一个常数，患者的原始视力将根据其是否患有病症以及使用的眼药水类型而相应增加或减少。更具体地说

如果 Condition = 0 且 Treatment = 1 则 Vision = N_V + P_2

如果 Condition = 0 且 Treatment = 2 则 Vision = N_V - P_2

如果 Condition = 1 且 Treatment = 1 则 Vision = N_V - P_2

如果 Condition = 1 且 Treatment = 2 则 Vision = N_V + P_2

如果 Condition = 0 且 Treatment = 0 则 Vision = N_V - P_1

如果 Condition = 1 且 Treatment = 0 则 Vision = N_V - P3

注意 对于反事实陈述，指定的函数因果模型必须相对于噪声可逆（例如，加性噪声模型）非常重要。或者，用户也可以指定真实模型和真实噪声。

对于像患有病症 (Condition=1，概率很低，只有 1%) 这样的罕见事件，需要大量样本来训练模型，以便准确反映这些罕见事件。这就是为什么我们在这里使用了 10000 个样本来生成患者数据库。

[7]:

from scipy.stats import bernoulli, norm, uniform
import numpy as np
from random import randint

n_unobserved = 10000
unobserved_data = {
   'N_T': np.array([randint(0, 2) for p in range(n_unobserved)]),
   'N_vision': np.random.uniform(0.4, 0.6, size=(n_unobserved,)),
   'N_C': bernoulli.rvs(0.01, size=n_unobserved)
}
P_1 = 0.2
P_2 = 0.15

def create_observed_medical_data(unobserved_data):
    observed_medical_data = {}
    observed_medical_data['Condition'] = unobserved_data['N_C']
    observed_medical_data['Treatment'] = unobserved_data['N_T']
    observed_medical_data['Vision'] = unobserved_data['N_vision'] + (-P_1)*(1 - observed_medical_data['Condition'])*(1 - observed_medical_data['Treatment'])*(2 - observed_medical_data['Treatment']) + (2*P_2)*(1 - observed_medical_data['Condition'])*(observed_medical_data['Treatment'])*(2 - observed_medical_data['Treatment']) + (P_2)*(1 - observed_medical_data['Condition'])*(observed_medical_data['Treatment'])*(1 - observed_medical_data['Treatment'])*(3 - observed_medical_data['Treatment']) + 0*(observed_medical_data['Condition'])*(1 - observed_medical_data['Treatment'])*(2 - observed_medical_data['Treatment']) + (-2*P_2)*(unobserved_data['N_C'])*(observed_medical_data['Treatment'])*(2 - observed_medical_data['Treatment']) + (-P_2)*(observed_medical_data['Condition'])*(observed_medical_data['Treatment'])*(1 - observed_medical_data['Treatment'])*(3 - observed_medical_data['Treatment'])
    return pd.DataFrame(observed_medical_data)

medical_data = create_observed_medical_data(unobserved_data)

生成爱丽丝的数据：她的初始视力的随机噪声，Condition=1 (因为她患有罕见过敏症) 和她最初决定选择 Treatment=2 (眼药水选项 2)。

[8]:


num_samples = 1
original_vision = np.random.uniform(0.4, 0.6, size=num_samples)
def generate_specific_patient_data(num_samples):
    return create_observed_medical_data({
    'N_T': np.full((num_samples,), 2),
    'N_C': bernoulli.rvs(1, size=num_samples),
    'N_vision': original_vision,
})

specific_patient_data = generate_specific_patient_data(num_samples)