因果推断及其与机器学习的联系教程(使用 DoWhy+EconML)#
本教程将逐步介绍如何使用 DoWhy+EconML 库进行因果推断。在此过程中,我们将重点介绍其与机器学习的联系——机器学习如何帮助构建因果效应估计器,以及因果推理如何帮助构建更稳健的机器学习模型。
从根本上来说是因果推断问题的数据科学问题示例:* A/B 实验:如果我更改算法,会提高成功率吗?* 政策决策:如果我们采用这种处理/政策,会带来更健康的患者/更多收入等吗?* 政策评估:基于我现在所知,我的政策是帮助了还是损害了?* 归因:人们购买是因为推荐算法吗?他们无论如何都会购买吗?
在本教程中,您将:* 学习因果推理为何对决策至关重要,以及预测任务与决策任务的区别。
通过因果推断的四个步骤亲手实践估计因果效应:建模、识别、估计和反驳。
了解 DoWhy+EconML 如何使用统计学和机器学习的最新方法,通过 4 行代码帮助您估计因果效应,并评估其对建模假设的鲁棒性。
通过 Jupyter Notebook 真实案例研究,了解在不同场景中应用因果推理,包括估计客户忠诚度计划对未来交易的影响、预测哪些用户会受到干预(例如广告)的积极影响、产品定价以及确定哪些因素对结果贡献最大。
了解因果推断与现代机器学习模型挑战之间的联系。
目录
1 为什么选择因果推断?
1.1 定义因果效应
1.2 预测与因果推断的区别
1.3 因果推断的两个基本挑战
2 因果推断的四个步骤
2.1 DoWhy+EconML 解决方案
2.2 一个神秘数据集:你能找出是否存在因果效应吗?
2.2.1 使用因果图对数据生成过程进行模型假设
2.2.2 基于因果模型识别目标数量的正确估计量
2.2.3 估计目标估计量
2.2.4 使用反驳测试检查估计的鲁棒性
3 使用 DoWhy+EconML 的案例研究
3.1 估计客户忠诚度计划的影响
3.2 在线公司的推荐 A/B 测试
3.3 用于干预目标定位的用户分段
3.4 软件公司的多项投资归因
4 与基本机器学习挑战的联系
5 更多资源
5.1 DoWhy+EconML 库
5.2 因果推断及其与机器学习的联系视频讲座
5.3 详细的 KDD 因果推断教程
5.4 关于因果关系和机器学习的书籍章节
5.5 微软因果关系与机器学习小组
为什么选择因果推断?#
许多关键的数据科学任务都与决策有关。数据科学家经常被要求支持各级决策者,帮助他们最好地利用数据来实现预期结果。例如,高管制定投资和资源决策、营销人员确定折扣政策、产品团队确定要发布的功能的优先级,或者医生决定为患者采取何种治疗方案。
这些决策者都在问“如果...会怎样”的问题。要用数据回答这类问题,需要理解事件的原因以及如何采取行动来改善未来结果。
定义因果效应#
假设我们想找出采取行动 A 对结果 Y 的因果效应。要定义因果效应,考虑两个世界:1. 世界 1(真实世界):采取了行动 A 并观测到 Y 2. 世界 2(反事实世界):未采取行动 A(但其他一切都相同)
因果效应是真实世界中获得的 Y 值与反事实世界中获得的 Y 值之间的差异。

换句话说,A 导致 Y 当且仅当改变 A 会导致 Y 的变化,同时保持其他一切恒定。在保持其他一切恒定的情况下改变 A 称为干预,并用特殊符号 \(do(A)\) 表示。
正式地,因果效应是 Y 由于 A 的单位干预性变化而改变的幅度
为了估计效应,黄金标准是进行随机实验,其中随机选择一部分单元进行干预(\(A=1\)),另一部分则不干预(\(A=0\))。这些子集近似于不相交的真实世界和反事实世界,并且随机化确保两个子集之间没有系统性差异(“保持其他一切恒定”)。
然而,进行随机实验并不总是可行。为了回答因果问题,我们通常需要依赖观测数据或日志数据。这类观测数据因相关性和未观测到的混杂因素而存在偏差,因此受到干预的单元和未受到干预的单元之间存在系统性差异。例如,新的营销活动可能在假日期间部署,新功能可能只应用于高活跃用户,或者老年患者更有可能接受新药等等。因果推断方法的目标是从数据中消除这些相关性和混杂因素,并估计行动的真实效应,如上式所示。
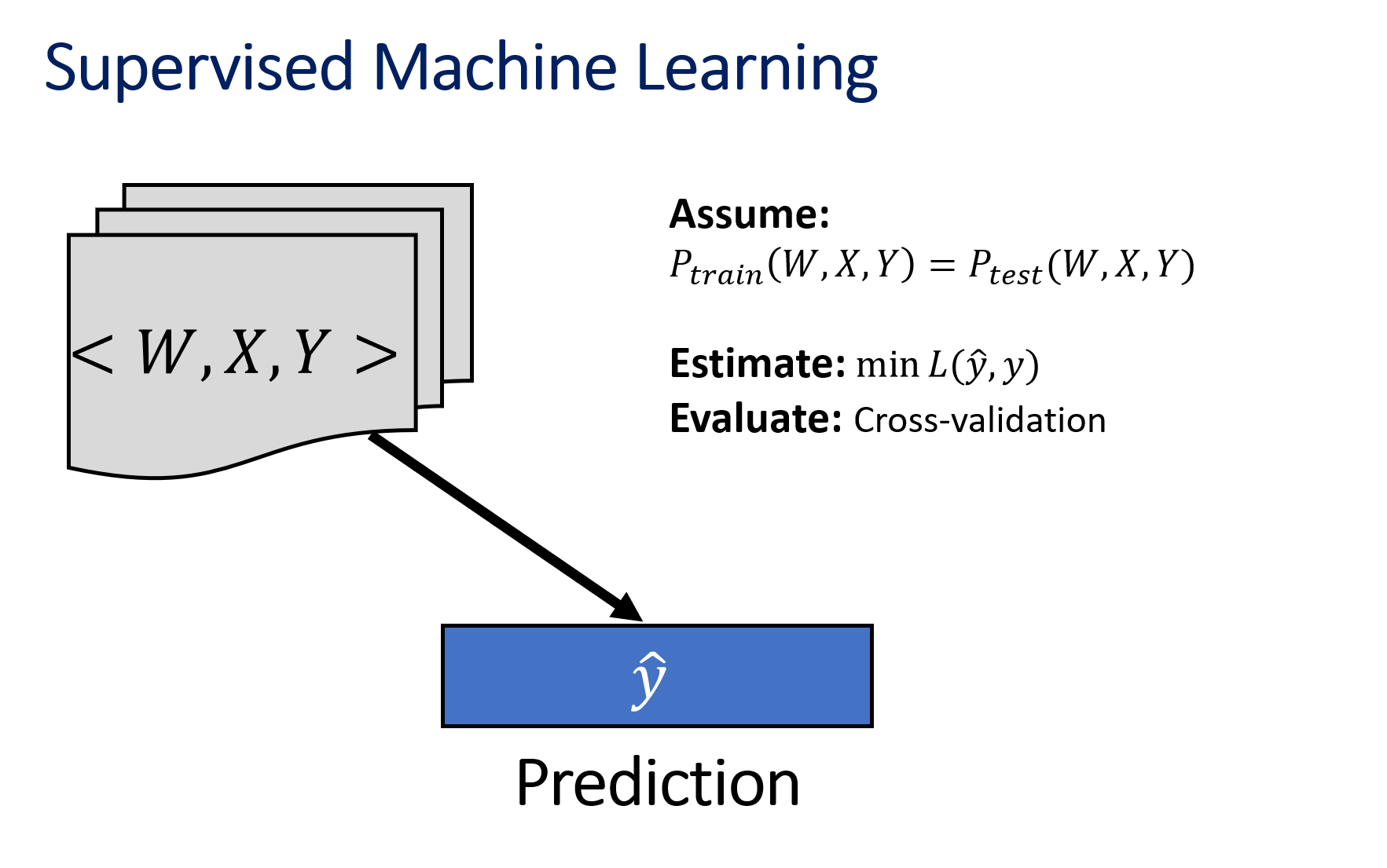
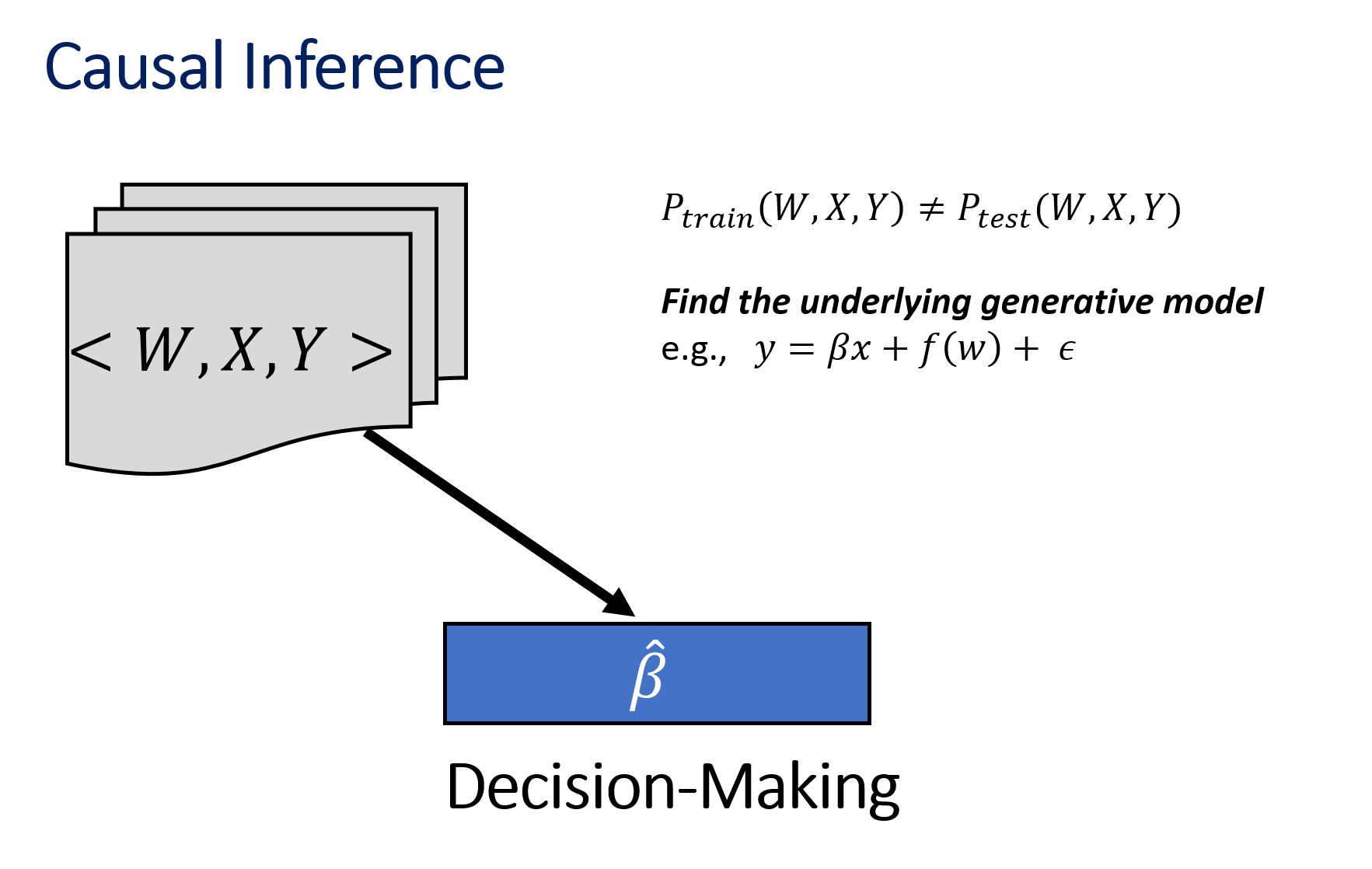
预测与因果推断的区别#
|
|
因果推断的两个基本挑战#
我们永远无法观测到反事实世界
无法直接计算因果效应
必须估计反事实
验证中的挑战
多种因果机制可以拟合单一数据分布 * 仅凭数据不足以进行因果推断 * 需要领域知识和假设
因果推断的四个步骤#
由于没有可用于比较估计值的真实测试数据集,因此因果推断需要一系列原则性步骤才能获得良好的估计器。
让我们通过一个示例数据集来阐述这四个步骤。本教程需要您下载两个库:DoWhy 和 EconML。两者都可以通过以下命令安装:pip install dowhy econml。
[1]:
# Required libraries
import dowhy
from dowhy import CausalModel
import dowhy.datasets
# Avoiding unnecessary log messges and warnings
import logging
logging.getLogger("dowhy").setLevel(logging.WARNING)
import warnings
from sklearn.exceptions import DataConversionWarning
warnings.filterwarnings(action='ignore', category=DataConversionWarning)
# Load some sample data
data = dowhy.datasets.linear_dataset(
beta=10,
num_common_causes=5,
num_instruments=2,
num_samples=10000,
treatment_is_binary=True,
stddev_treatment_noise=10)
一、建模
第一步是将我们的领域知识编码到因果模型中,通常表示为图。因果推断分析的最终结果很大程度上取决于输入假设,因此这一步非常重要。为了估计因果效应,大多数常见问题涉及指定两种类型的变量
混杂因素 (common_causes):这些变量同时导致行动和结果。因此,行动和结果之间观察到的任何相关性可能仅仅是由于混杂变量造成的,而不是行动与结果之间的任何因果关系造成的。
工具变量 (instruments):这些是特殊变量,它们导致行动,但不会直接影响结果。此外,它们不受任何影响结果的变量的影响。如果使用正确,工具变量可以帮助减少偏差。
[2]:
# I. Create a causal model from the data and domain knowledge.
model = CausalModel(
data=data["df"],
treatment=data["treatment_name"],
outcome=data["outcome_name"],
common_causes=data["common_causes_names"],
instruments=data["instrument_names"])
为了可视化图,我们可以写:
[3]:
model.view_model(layout="dot")
from IPython.display import Image, display
display(Image(filename="causal_model.png"))
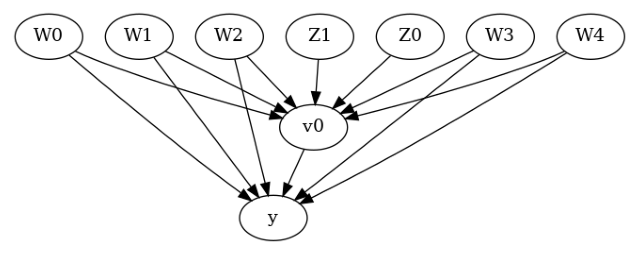
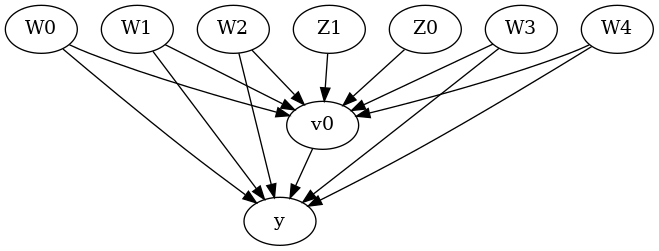
通常,您可以指定一个因果图来描述给定数据集的数据生成过程机制。图中的每个箭头都表示一种因果机制:“A->B”意味着变量 A 导致变量 B。
[4]:
# I. Create a causal model from the data and given graph.
model = CausalModel(
data=data["df"],
treatment=data["treatment_name"][0],
outcome=data["outcome_name"][0],
graph=data["gml_graph"])
model.view_model(layout="dot")
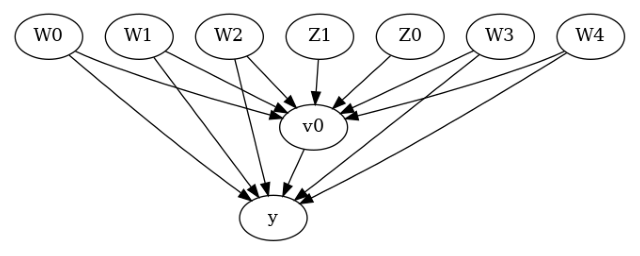
二、识别
提供领域知识的两种方式(无论是通过指定混杂因素和工具变量的变量集,还是通过因果图)都对应于一个潜在的因果图。给定一个因果图和目标数量(例如,A 对 B 的影响),识别过程就是检查给定观测变量是否可以估计目标数量。重要的是,识别只考虑观测数据中可用的变量名称;它不需要访问数据本身。与上述两种变量类型相关,因果推断有两种主要的识别方法。
后门准则(或更广泛地说,调整集):如果行动 A 和结果 Y 的所有共同原因都已观测到,那么后门准则意味着可以通过条件化所有共同原因来识别因果效应。这是一个简化定义(有关正式定义,请参阅 CausalML 书籍的第 3 章)。
\[E[Y│do(A=a)] = E_W E[Y|A=a, W=w]\]
其中 \(W\) 指的是 \(A\) 和 \(Y\) 的共同原因(混杂因素)的集合。
工具变量 (IV) 识别:如果存在工具变量,即使行动和结果的共同原因有任何(或没有)未观测到,我们也可以估计效应。IV 识别利用了工具变量只直接影响行动的事实,因此工具变量对结果的影响可以分解为两个顺序部分:工具变量对行动的影响以及行动对处理的影响。然后,它依赖于估计工具变量对行动和结果的影响来估计行动对结果的影响。对于二元工具变量,效应估计值由下式给出:
[5]:
# II. Identify causal effect and return target estimands
identified_estimand = model.identify_effect(proceed_when_unidentifiable=True)
print(identified_estimand)
Estimand type: EstimandType.NONPARAMETRIC_ATE
### Estimand : 1
Estimand name: backdoor
Estimand expression:
d
─────(E[y|W3,W4,W1,W2,W0])
d[v₀]
Estimand assumption 1, Unconfoundedness: If U→{v0} and U→y then P(y|v0,W3,W4,W1,W2,W0,U) = P(y|v0,W3,W4,W1,W2,W0)
### Estimand : 2
Estimand name: iv
Estimand expression:
⎡ -1⎤
⎢ d ⎛ d ⎞ ⎥
E⎢─────────(y)⋅⎜─────────([v₀])⎟ ⎥
⎣d[Z₁ Z₀] ⎝d[Z₁ Z₀] ⎠ ⎦
Estimand assumption 1, As-if-random: If U→→y then ¬(U →→{Z1,Z0})
Estimand assumption 2, Exclusion: If we remove {Z1,Z0}→{v0}, then ¬({Z1,Z0}→y)
### Estimand : 3
Estimand name: frontdoor
No such variable(s) found!
三、估计
顾名思义,估计步骤涉及构建一个统计估计器,该估计器可以计算上一步中识别出的目标估计量。已经提出了许多用于因果推断的估计器。DoWhy 实现了一些标准估计器,而 EconML 实现了一套强大的使用机器学习的估计器。
我们展示了使用 DoWhy 进行倾向得分分层,以及使用 EconML 进行称为 Double-ML 的基于机器学习的方法的示例。
[6]:
# III. Estimate the target estimand using a statistical method.
propensity_strat_estimate = model.estimate_effect(identified_estimand,
method_name="backdoor.dowhy.propensity_score_stratification")
print(propensity_strat_estimate)
*** Causal Estimate ***
## Identified estimand
Estimand type: EstimandType.NONPARAMETRIC_ATE
### Estimand : 1
Estimand name: backdoor
Estimand expression:
d
─────(E[y|W3,W4,W1,W2,W0])
d[v₀]
Estimand assumption 1, Unconfoundedness: If U→{v0} and U→y then P(y|v0,W3,W4,W1,W2,W0,U) = P(y|v0,W3,W4,W1,W2,W0)
## Realized estimand
b: y~v0+W3+W4+W1+W2+W0
Target units: ate
## Estimate
Mean value: 9.992994156114678
[7]:
import econml
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LassoCV
from sklearn.ensemble import GradientBoostingRegressor
dml_estimate = model.estimate_effect(identified_estimand,
method_name="backdoor.econml.dml.DML",
method_params={
'init_params': {'model_y':GradientBoostingRegressor(),
'model_t': GradientBoostingRegressor(),
'model_final':LassoCV(fit_intercept=False), },
'fit_params': {}
})
print(dml_estimate)
*** Causal Estimate ***
## Identified estimand
Estimand type: EstimandType.NONPARAMETRIC_ATE
### Estimand : 1
Estimand name: backdoor
Estimand expression:
d
─────(E[y|W3,W4,W1,W2,W0])
d[v₀]
Estimand assumption 1, Unconfoundedness: If U→{v0} and U→y then P(y|v0,W3,W4,W1,W2,W0,U) = P(y|v0,W3,W4,W1,W2,W0)
## Realized estimand
b: y~v0+W3+W4+W1+W2+W0 |
Target units: ate
## Estimate
Mean value: 9.992748891600764
Effect estimates: [[9.99274889]]
四、反驳
最后,检查估计的鲁棒性可能是因果分析中最重要的一步。我们使用步骤 1-3 获得了估计值,但每一步都可能做出某些可能不正确的假设。由于缺乏适当的验证“测试”集,这一步依赖于反驳测试,这些测试试图使用一个好的估计器的属性来反驳所获得的估计值的正确性。例如,一个反驳测试(placebo_treatment_refuter)检查当行动变量被一个与所有其他变量独立的随机变量替换时,估计器是否返回 0 的估计值。
[8]:
# IV. Refute the obtained estimate using multiple robustness checks.
refute_results = model.refute_estimate(identified_estimand, propensity_strat_estimate,
method_name="placebo_treatment_refuter")
print(refute_results)
Refute: Use a Placebo Treatment
Estimated effect:9.992994156114678
New effect:-0.006921466905131964
p value:0.96
DoWhy+EconML 解决方案#
我们将使用 DoWhy+EconML 库进行因果推断。DoWhy 为这四个步骤提供了通用 API,而 EconML 为估计步骤提供了高级估计器。
DoWhy 允许您可视化、形式化和测试它们正在做的假设,以便您更好地理解分析并避免得出错误的结论。它通过明确关注假设并在可能的情况下引入对假设有效性的自动化检查来实现这一点。您将看到,DoWhy 的强大之处在于它提供了一个形式化的因果框架来编码领域知识,并且可以运行自动化鲁棒性检查来验证任何估计器方法得出的因果估计。
此外,随着数据维度变高,我们需要能够处理已知混杂因素的专门方法。这里我们使用 EconML,它实现了许多最先进的因果估计方法。该包为所有技术提供了通用 API,并且每种技术都实现为一系列机器学习任务,允许使用任何现有机器学习软件来解决这些子任务,从而允许您插入您已经熟悉的机器学习模型,而不是学习新的工具包。EconML 的强大之处在于,您现在可以像运行线性回归或随机森林一样轻松地实现因果推断的最新技术。
总之,DoWhy+EconML 通过提供一个最先进的端到端因果推断框架,包括最新的因果估计和自动化鲁棒性程序,使得回答“如果...会怎样”的问题变得容易得多。
一个神秘数据集:你能找出是否存在因果效应吗?#
为了逐步介绍这四个步骤,让我们考虑神秘数据集问题。假设您获得了一些包含处理和结果的数据。您能确定处理是否导致了结果,还是相关性纯粹是由于另一个共同原因造成的?
[9]:
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import math
import dowhy.datasets, dowhy.plotter
下面我们创建一个数据集,其中真实的因果效应由随机变量决定。它可以是 0 或 1。
[10]:
rvar = 1 if np.random.uniform() > 0.2 else 0
is_linear = False # A non-linear dataset. Change to True to see results for a linear dataset.
data_dict = dowhy.datasets.xy_dataset(10000, effect=rvar,
num_common_causes=2,
is_linear=is_linear,
sd_error=0.2)
df = data_dict['df']
print(df.head())
dowhy.plotter.plot_treatment_outcome(df[data_dict["treatment_name"]], df[data_dict["outcome_name"]],
df[data_dict["time_val"]])
Treatment Outcome w0 s w1
0 17.098831 34.939507 -3.377379 0.283867 0.504289
1 18.320187 37.218290 3.418561 2.237479 1.102549
2 14.073424 28.034111 -2.808841 8.091403 0.161078
3 9.691199 20.592411 1.853534 4.465082 1.562526
4 8.888019 18.451855 1.693628 4.518675 0.698603
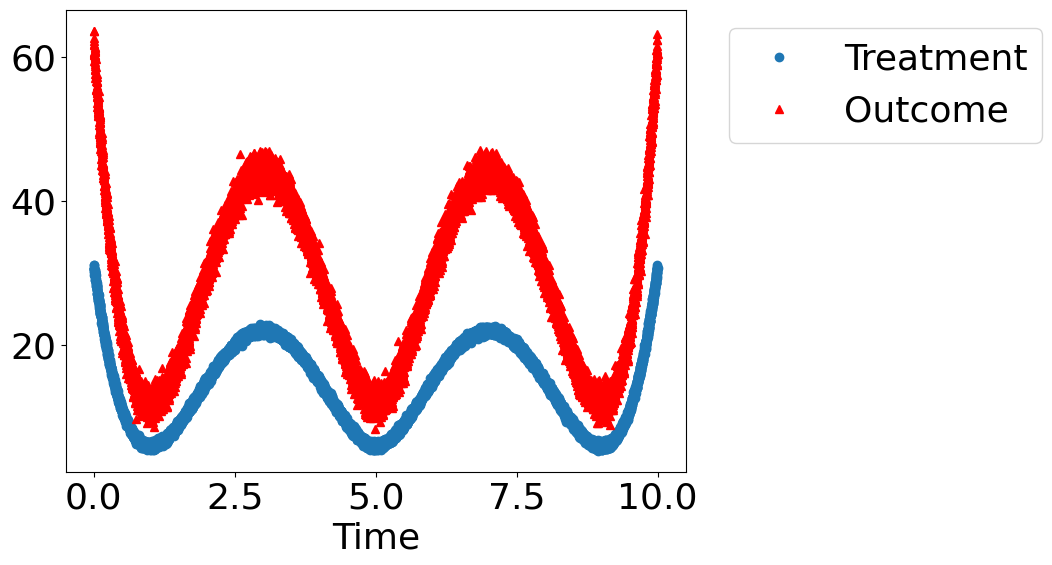
使用因果图对数据生成过程进行模型假设#
[11]:
model= CausalModel(
data=df,
treatment=data_dict["treatment_name"],
outcome=data_dict["outcome_name"],
common_causes=data_dict["common_causes_names"],
instruments=data_dict["instrument_names"])
model.view_model(layout="dot")
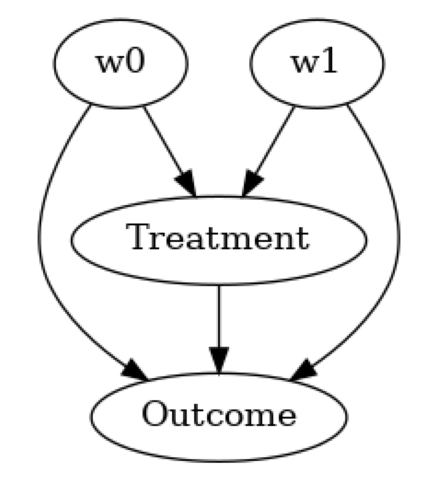
基于因果模型识别目标数量的正确估计量#
[12]:
identified_estimand = model.identify_effect(proceed_when_unidentifiable=True)
print(identified_estimand)
Estimand type: EstimandType.NONPARAMETRIC_ATE
### Estimand : 1
Estimand name: backdoor
Estimand expression:
d
────────────(E[Outcome|w0,w1])
d[Treatment]
Estimand assumption 1, Unconfoundedness: If U→{Treatment} and U→Outcome then P(Outcome|Treatment,w0,w1,U) = P(Outcome|Treatment,w0,w1)
### Estimand : 2
Estimand name: iv
No such variable(s) found!
### Estimand : 3
Estimand name: frontdoor
No such variable(s) found!
由于这是观测数据,警告会询问您此数据集中是否存在任何缺失的未观测混杂因素。如果存在,忽略它们将导致估计不正确。如果您想禁用警告,可以在 identify_effect 中添加额外参数 proceed_when_unidentifiable=True。
估计目标估计量#
[13]:
estimate = model.estimate_effect(identified_estimand,
method_name="backdoor.linear_regression")
print(estimate)
print("Causal Estimate is " + str(estimate.value))
# Plot Slope of line between action and outcome = causal effect
dowhy.plotter.plot_causal_effect(estimate, df[data_dict["treatment_name"]], df[data_dict["outcome_name"]])
*** Causal Estimate ***
## Identified estimand
Estimand type: EstimandType.NONPARAMETRIC_ATE
### Estimand : 1
Estimand name: backdoor
Estimand expression:
d
────────────(E[Outcome|w0,w1])
d[Treatment]
Estimand assumption 1, Unconfoundedness: If U→{Treatment} and U→Outcome then P(Outcome|Treatment,w0,w1,U) = P(Outcome|Treatment,w0,w1)
## Realized estimand
b: Outcome~Treatment+w0+w1
Target units: ate
## Estimate
Mean value: 1.9984660510163166
Causal Estimate is 1.9984660510163166
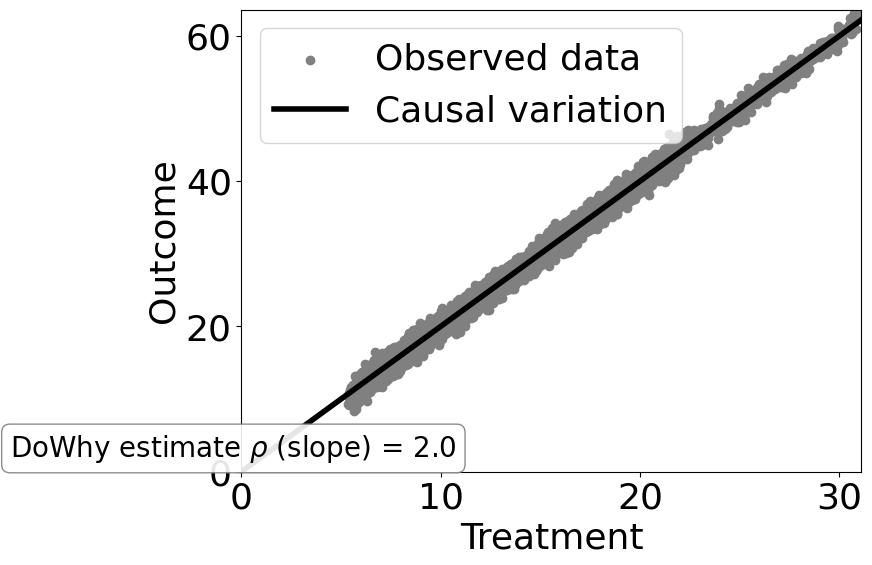
如您所见,对于非线性数据生成过程,线性回归模型无法将因果效应与观测到的相关性区分开来。
然而,如果 DGP 是线性的,那么简单的线性回归就可以工作。为了看到这一点,尝试将上面单元格 10 中的 is_linear=True。
为了对非线性数据(以及具有高维混杂因素的数据)进行建模,我们需要更高级的方法。下面是使用 EconML 中的双重机器学习估计器的一个示例。该估计器使用诸如梯度提升树之类的基于机器学习的方法来学习结果与混杂因素、以及处理与混杂因素之间的关系,然后最终比较结果与处理之间的残差变异。
[14]:
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LassoCV
from sklearn.ensemble import GradientBoostingRegressor
dml_estimate = model.estimate_effect(identified_estimand, method_name="backdoor.econml.dml.DML",
control_value = 0,
treatment_value = 1,
confidence_intervals=False,
method_params={"init_params":{'model_y':GradientBoostingRegressor(),
'model_t': GradientBoostingRegressor(),
"model_final":LassoCV(fit_intercept=False),
'featurizer':PolynomialFeatures(degree=2, include_bias=True)},
"fit_params":{}})
print(dml_estimate)
*** Causal Estimate ***
## Identified estimand
Estimand type: EstimandType.NONPARAMETRIC_ATE
### Estimand : 1
Estimand name: backdoor
Estimand expression:
d
────────────(E[Outcome|w0,w1])
d[Treatment]
Estimand assumption 1, Unconfoundedness: If U→{Treatment} and U→Outcome then P(Outcome|Treatment,w0,w1,U) = P(Outcome|Treatment,w0,w1)
## Realized estimand
b: Outcome~Treatment+w0+w1 |
Target units: ate
## Estimate
Mean value: 1.0899098944494576
Effect estimates: [[1.08990989]]
如您所见,DML 方法获得了更好的估计,更接近真实的因果效应 1。
使用反驳测试检查估计的鲁棒性#
[15]:
res_random=model.refute_estimate(identified_estimand, dml_estimate, method_name="random_common_cause")
print(res_random)
Refute: Add a random common cause
Estimated effect:1.0899098944494576
New effect:1.085246993578022
p value:0.96
[16]:
res_placebo=model.refute_estimate(identified_estimand, dml_estimate,
method_name="placebo_treatment_refuter", placebo_type="permute",
num_simulations=20)
print(res_placebo)
Refute: Use a Placebo Treatment
Estimated effect:1.0899098944494576
New effect:-0.00016849220899518638
p value:0.39172166125577124
使用 DoWhy+EconML 的案例研究#
在实践中,随着数据维度变高,简单的估计器将无法估计正确的因果效应。更高级的监督机器学习模型也无法工作,而且通常比简单的回归更差,因为它们包含了有助于最小化预测误差的额外正则化技术,但这可能对估计因果效应产生不良影响。因此,我们需要专门针对估计因果效应的方法。同时,我们还需要合适的反驳方法来检查估计的鲁棒性。
这里是使用 DoWhy+EconML 处理高维数据集的一个示例。
更多详细信息请参阅此 notebook。
下面我们提供案例研究链接,这些案例研究说明了 DoWhy+EconML 的使用。
估计客户忠诚度计划的影响#
在线公司的推荐 A/B 测试#
用于干预目标定位的用户分段#
软件公司的多项投资归因#
与基本机器学习挑战的联系#
因果关系与构建机器学习模型中的许多基本挑战相关,包括分布外泛化、公平性、可解释性和隐私。

因果关系如何帮助解决上述许多挑战是一个活跃的研究领域。
更多资源#
DoWhy+EconML 库#
DoWhy 代码:microsoft/dowhy
DoWhy notebook:microsoft/dowhy
EconML 代码:microsoft/econml
EconML notebook:microsoft/EconML
因果推断及其与机器学习的联系视频讲座#
微软研究院网络研讨会:https://note.microsoft.com/MSR-Webinar-DoWhy-Library-Registration-On-Demand.html
详细的 KDD 因果推断教程#
关于因果关系和机器学习的书籍章节#
微软因果关系与机器学习小组#
https://www.microsoft.com/en-us/research/group/causal-inference/