使用 OverRule 评估支持和重叠#
动机#
在执行后门调整时,即使我们正确指定了因果图并观察到所有相关的后门调整变量 \(X\),我们只能估计满足以下两个条件的协变量 \(X\) 个体的因果效应:* 支持:简单来说,我们要求在我们的数据集中观察到类似的个体。对于离散协变量 \(X\),这可以形式化为要求
* 重叠:我们要求对于相似的个体,存在观察到处理和对照的可能性。形式上,我们要求
OverRule [1] 是一种学习布尔规则集的方法,用于表征满足这两个条件的个体集合,并在本笔记本中通过一些简单的示例来构建直觉。
致谢#
OverRule 的代码改编自 (clinicalml/overlap-code),进行了最小修改和一些简化,遵循 MIT 许可证。
[1] Oberst, M., Johansson, F., Wei, D., Gao, T., Brat, G., Sontag, D., & Varshney, K. (2020). 观测研究中重叠的表征。载于 S. Chiappa & R. Calandra (编著),第二十三届国际人工智能与统计会议论文集(第 108 卷,页 788–798)。PMLR。https://arxiv.org/abs/1907.04138
目录#
简单二维示例图示
问题数据
使用默认参数应用 OverRule
解释 OverRule 的输出
配置 OverRule
Lalonde 和 PSID 数据集图示
[1]:
import numpy as np
import pandas as pd
import dowhy.datasets
from dowhy import CausalModel
# Functional API
from dowhy.causal_refuters.assess_overlap import assess_support_and_overlap_overrule
# Data classes to configure ruleset optimization
from dowhy.causal_refuters.assess_overlap_overrule import SupportConfig, OverlapConfig
import matplotlib.pyplot as plt
简单二维示例图示#
返回目录
问题数据#
返回目录
在此示例中,我们有一对二元协变量 \(X_1, X_2\),它们简单地违反了上述条件:* 支持:没有 \(X_1 = X_2 = 1\) 的样本,即 \(P(X_1 = 1, X_2 = 1) = 0\) * 重叠:只有 \(X_1 = 0, X_2 = 0\) 的个体有机会同时接受处理 \((T = 1)\) 和对照 \((T = 0)\)
[2]:
test_data = pd.DataFrame(
np.array(
[
[0, 0, 1, 1],
[0, 0, 0, 0],
[0, 1, 1, 0],
[1, 0, 0, 0],
]
* 50
),
columns=["X1", "X2", "T", "Y"],
)
我们可以按如下方式可视化这些模式,其中我们添加了一些扰动以便更容易看到
[3]:
rng = np.random.default_rng(0)
jitter_data = test_data.copy()
jitter_data['X1'] = jitter_data['X1'] + rng.normal(0, 0.05, size=(200,))
jitter_data['X2'] = jitter_data['X2'] + rng.normal(0, 0.05, size=(200,))
fig, ax = plt.subplots(1, 1, figsize=(5, 5))
for t in [0, 1]:
this_data = jitter_data.query('T == @t')
ax.scatter(this_data['X1'], this_data['X2'], label=f'T = {t}', edgecolor='w', linewidths=0.5)
plt.legend()
plt.show()
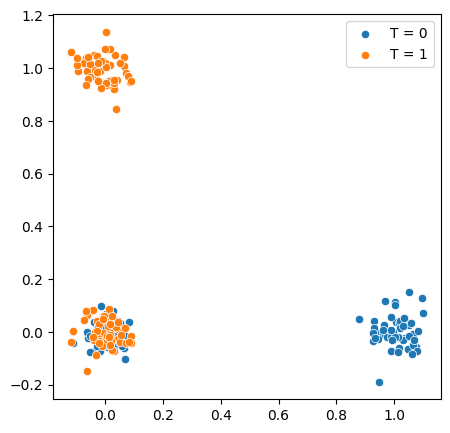
注意,重叠区域仅在 \(X_1 = X_2 = 0\) 时成立。
使用默认参数应用 OverRule#
返回目录
此方法目前实现为一种反驳方法,但也可以通过函数式 API 访问。下面我们演示这两种方法,然后讨论它们的参数。
请注意,OverRule 返回析取范式 (DNF) 规则,可以理解为 OR 的 AND,并在调用 print(refute) 时给出。
使用 CausalModel 的示例用法#
[4]:
model = CausalModel(
data=test_data,
treatment="T",
outcome="Y",
common_causes=['X1', 'X2']
)
[5]:
identified_estimand = model.identify_effect(proceed_when_unidentifiable=True)
estimate = model.estimate_effect(identified_estimand, method_name="backdoor.linear_regression")
[6]:
# We disucss configuration in more depth below.
support_config = SupportConfig(seed=0)
overlap_config = OverlapConfig()
[7]:
refute = model.refute_estimate(
identified_estimand,
estimate,
method_name='assess_overlap',
support_config=support_config,
overlap_config=overlap_config,
)
[8]:
print(refute)
Rules cover 50.0% of all samples
Overall, 50.0% of samples meet the criteria for inclusion in the overlap set,
defined as (a) being covered by support rules and having propensity
score in (0.10, 0.90)
Rules capture 100.0% of samples which meet these criteria
How to read rules: The following rules are given in Disjuntive Normal Form,
a series of AND clauses (e.g., X and Y and Z) joined by ORs. Hence, if a sample
satifies any of the clauses for the support rules, it is included in the support,
and likewise for the overlap rules.
DETAILED RULES:
SUPPORT Rules: Found 2 rule(s), covering 100.0% of samples
Rule #0: (not X1)
[Covers 75.0% of samples]
OR Rule #1: (X1)
AND (not X2)
[Covers 25.0% of samples]
OVERLAP Rules: Found 1 rule(s), covering 50.0% of samples
Rule #0: (not X1)
AND (not X2)
[Covers 50.0% of samples]
使用函数式 API 的示例用法#
请注意,结果 \(Y\) 未用作 OverRule 的一部分,因此在此处不需要。
[9]:
refute = assess_support_and_overlap_overrule(
data=test_data,
backdoor_vars=['X1', 'X2'],
treatment_name='T',
support_config=support_config,
overlap_config=overlap_config
)
只拟合支持或重叠规则#
您还可以通过传递 support_only=True 或 overlap_only=True 来运行 OverRule,以便仅学习支持或重叠规则。
[10]:
refute = model.refute_estimate(
identified_estimand,
estimate,
method_name='assess_overlap',
support_only=True,
support_config=support_config,
)
[11]:
print(refute)
Rules cover 100.0% of all samples
How to read rules: The following rules are given in Disjuntive Normal Form,
a series of AND clauses (e.g., X and Y and Z) joined by ORs. Hence, if a sample
satifies any of the clauses for the support rules, it is included in the support,
and likewise for the overlap rules.
DETAILED RULES:
SUPPORT Rules: Found 2 rule(s), covering 100.0% of samples
Rule #0: (not X1)
[Covers 75.0% of samples]
OR Rule #1: (X1)
AND (not X2)
[Covers 25.0% of samples]
No Overlap Rules Fitted (support_only=True).
[12]:
refute = model.refute_estimate(
identified_estimand,
estimate,
method_name='assess_overlap',
overlap_only=True,
overlap_config=overlap_config
)
[13]:
print(refute)
Rules cover 50.0% of all samples
Overall, 50.0% of samples meet the criteria for inclusion in the overlap set,
defined as (a) being covered by support rules and having propensity
score in (0.10, 0.90)
Rules capture 100.0% of samples which meet these criteria
How to read rules: The following rules are given in Disjuntive Normal Form,
a series of AND clauses (e.g., X and Y and Z) joined by ORs. Hence, if a sample
satifies any of the clauses for the support rules, it is included in the support,
and likewise for the overlap rules.
DETAILED RULES:
No Support Rules Fitted (overlap_only=True).
OVERLAP Rules: Found 1 rule(s), covering 50.0% of samples
Rule #0: (not X1)
AND (not X2)
[Covers 50.0% of samples]
解释 OverRule 的输出#
返回目录
我们将使用以下规则集来说明如何解释输出。
SUPPORT Rules: Found 2 rule(s), covering 100.0% of samples
Rule #0: (not X1)
[Covers 75.0% of samples]
OR Rule #1: (X1)
AND (not X2)
[Covers 25.0% of samples]
OVERLAP Rules: Found 1 rule(s), covering 50.0% of samples
Rule #0: (not X2)
AND (not X1)
[Covers 50.0% of samples]
对于任何样本,我们可以通过检查每个规则(规则 0 和规则 1)来检查该样本是否被支持覆盖。如果这些规则中的任意一条适用,则该样本在支持内。考虑一个点 (X1 = 1, X2 = 1),我们知道它不在原始数据的支持中。由于每个二元输入被视为布尔值,我们可以检查:* 规则 0: (not X1) –> 此规则不被 (X1 = 1, X2 = 1) 满足,因为 X1 = 1 等同于 X2 = True * 规则 1: (X1) AND (not X2) –> 此规则不被满足,因为 X2 = 1
同样,我们可以检查一个样本是否被重叠规则覆盖。考虑点 (X1 = 1, X2 = 0)。它满足支持规则,因为它匹配规则 0。然而,对于重叠规则,我们可以检查:* 规则 0: (not X2) AND (not X1) –> 此规则不被满足,因为 X1 = 1。
注意:当我们稍后基于 OverRule 学习到的规则过滤样本时,我们将过滤掉任何不同时匹配支持规则和重叠规则的样本。
配置 OverRule#
返回目录
OverRule 可以通过传递以下参数进行配置:* overlap_eps:这是一个位于 (0, 0.5) 中的数字 \(\epsilon\),它将重叠区域定义为 \(P(T = 1 \mid X)\) 位于 \((\epsilon, 1 - \epsilon)\) 中的点。
cat_feats:任何类别特征的列表(如果 dtype 是 object 则自动推断)。support_config:一个SupportConfig(见下文),控制优化参数。overlap_config:一个OverlapConfig(见下文),控制优化参数。
[14]:
support_config = SupportConfig()
print(support_config)
SupportConfig(n_ref_multiplier=1.0, seed=None, alpha=0.98, lambda0=0.01, lambda1=0.001, K=20, D=20, B=10, iterMax=10, num_thresh=9, thresh_override=None, solver='ECOS', rounding='greedy_sweep')
[15]:
overlap_config = OverlapConfig()
print(overlap_config)
OverlapConfig(alpha=0.95, lambda0=0.001, lambda1=0.001, K=20, D=20, B=10, iterMax=10, num_thresh=9, thresh_override=None, solver='ECOS', rounding='greedy_sweep')
关键参数:对于 SupportConfig 和 OverlapConfig,默认值通常是合理的,但根据问题可能需要更改一些参数,详细如下。
alpha:对于学习支持规则,我们要求至少包含原始数据的
alpha分数,同时最小化所得支持集的体积。对于学习重叠规则,至少包含“重叠点”的
alpha分数,同时排除尽可能多的非重叠点。此处,“重叠点”定义为那些 \(P(T = 1 \mid X)\) 位于[overlap_eps, 1 - overlap_eps]范围内(使用 XGBClassifier 估计)的点。
lambda0,lambda1:这些是控制最终规则复杂度的正则化项。lambda0是为每个新规则添加的惩罚(一个规则可以包含多个文字)。例如,(not X1) AND (not X2)是一个单一规则。lambda1是为每个文字添加的惩罚。例如,(not X1) AND (not X2)包含两个文字。
num_thresh:OverRule 在学习规则集之前将所有特征转换为二元规则。对于连续变量,默认情况下通过转换为十分位数来实现。可以通过更改阈值数量或指定一个字典(在thresh_override中)将特征映射到阈值的np.ndarray来更改此默认行为。
Lalonde 和 PSID 数据集图示#
返回目录
本节展示了如何在进行另一项因果分析的过程中应用 OverRule。此处,我们演示了两种方法:* 在进行任何因果效应估计之前应用 OverRule * 使用学习到的规则过滤样本
将 OverRule 纳入因果推断工作流程如下所示:* 首先,在执行任何因果效应估计之前,应用 OverRule 来学习规则 * 其次,根据学习到的规则过滤样本 * 第三,在过滤后的样本上估计因果效应
为了说明这一点,我们使用两个数据集构建了一个有点人工的因果推断任务:* 来自 Lalonde (1986) 的原始数据集,其中包含实验样本,通过 dowhy.datasets.lalonde_dataset() 加载。由于这是实验样本,我们将看到重叠在该样本中的所有样本上都成立。 * 一个完全由未处理样本组成的观测数据集,即 PSID 数据集,在 Smith & Todd (2005) 中结合原始实验数据集进行了分析。它从 dowhy.datasets.psid_dataset() 加载。
通过合并这些数据集然后评估重叠,我们发现在合并的数据集中,重叠仅在约 30% 的样本中成立。 直观地说,许多来自 PSID 的样本被排除,这是由于原始实验的严格纳入标准所致。
[48]:
import pandas as pd
import dowhy.datasets
from dowhy.causal_refuters.assess_overlap import assess_support_and_overlap_overrule
from dowhy.causal_refuters.assess_overlap_overrule import OverlapConfig, SupportConfig
# Experimental sample from Lalonde
experiment_data = dowhy.datasets.lalonde_dataset()
# Observational sample
observational_controls = dowhy.datasets.psid_dataset()
experiment_data["exp_samp"] = True
observational_controls["exp_samp"] = False
data = pd.concat([experiment_data, observational_controls], axis=0, ignore_index=True)
support_config = SupportConfig(seed=0, lambda0=0.01, lambda1=0.01)
overlap_config = OverlapConfig(lambda0=0.01, lambda1=0.01)
在运行任何因果分析之前,我们首先检查支持和重叠。请注意,alpha 的默认设置为 0.98,这意味着:* 支持规则将尝试覆盖至少 98% (alpha) 的数据,且体积最小。* 重叠规则将尝试覆盖至少 98% (alpha) 具有倾向得分在 [overlap_eps, 1-overlap_eps] 范围内的样本。
检查实验样本中的支持/重叠#
[17]:
refute_experiment = assess_support_and_overlap_overrule(
data=experiment_data,
backdoor_vars="nodegr+black+hisp+age+educ+married+re74+re75".split("+"),
treatment_name="treat",
support_config=support_config,
overlap_config=overlap_config,
)
# Observe how everyone is in the overlap set, so we do not learn any overlap rules
print(refute_experiment)
All samples in the support region satisfy the overlap condition.
No Overlap Rules will be learned.
Rules cover 98.9% of all samples
How to read rules: The following rules are given in Disjuntive Normal Form,
a series of AND clauses (e.g., X and Y and Z) joined by ORs. Hence, if a sample
satifies any of the clauses for the support rules, it is included in the support,
and likewise for the overlap rules.
DETAILED RULES:
SUPPORT Rules: Found 4 rule(s), covering 98.9% of samples
Rule #0: ([re74 <= 0.000])
[Covers 73.3% of samples]
OR Rule #1: (black)
AND (not hisp)
AND ([age <= 35.000])
AND ([educ <= 12.000])
[Covers 71.5% of samples]
OR Rule #2: (not married)
AND ([re74 <= 7838.192])
AND ([re75 <= 5146.040])
[Covers 73.7% of samples]
OR Rule #3: (not black)
AND ([age <= 30.000])
AND ([educ <= 12.000])
AND ([educ > 8.000])
[Covers 10.6% of samples]
No Overlap Rules Fitted (support_only=True).
注意:如上所示,如果 OverRule 发现所有样本都满足重叠条件,则不会麻烦地学习单独的重叠规则。
评估合并样本中的支持/重叠#
现在,分析合并数据集,我们发现存在显著的重叠不足。
[18]:
var_list = "nodegr+black+hisp+age+educ+married+re74+re75".split("+")
refute = assess_support_and_overlap_overrule(
data=data,
backdoor_vars=var_list,
treatment_name="treat",
support_config=support_config,
overlap_config=overlap_config,
)
print(refute)
Rules cover 34.6% of all samples
Overall, 31.2% of samples meet the criteria for inclusion in the overlap set,
defined as (a) being covered by support rules and having propensity
score in (0.10, 0.90)
Rules capture 96.8% of samples which meet these criteria
How to read rules: The following rules are given in Disjuntive Normal Form,
a series of AND clauses (e.g., X and Y and Z) joined by ORs. Hence, if a sample
satifies any of the clauses for the support rules, it is included in the support,
and likewise for the overlap rules.
DETAILED RULES:
SUPPORT Rules: Found 2 rule(s), covering 98.1% of samples
Rule #0: ([re74 <= 33307.536])
AND ([re75 <= 32691.290])
[Covers 87.6% of samples]
OR Rule #1: (not nodegr)
AND (not hisp)
AND ([educ > 11.000])
[Covers 60.6% of samples]
OVERLAP Rules: Found 5 rule(s), covering 35.3% of samples
Rule #0: ([re74 <= 1282.723])
[Covers 20.0% of samples]
OR Rule #1: ([re75 <= 716.129])
[Covers 20.1% of samples]
OR Rule #2: (black)
AND (not married)
[Covers 15.2% of samples]
OR Rule #3: (not nodegr)
AND ([re74 <= 7837.067])
[Covers 12.2% of samples]
OR Rule #4: ([age <= 26.000])
AND ([educ > 11.000])
AND ([re75 <= 11637.097])
[Covers 7.7% of samples]
在进行因果分析前使用 OverRule 进行过滤#
OverRule 可以接受与原始数据框具有相同列的任何数据框,并过滤到包含在支持区域和重叠区域中的单元。
[56]:
bool_mask = refute.predict_overlap_support(data)
# This is a simple wrapper around refute.predict_overlap_support
filtered_df = refute.filter_dataframe(data).copy()
assert np.array_equal(data[bool_mask], filtered_df)
[47]:
bool_mask.mean()
[47]:
过滤后进行因果推断#
假设我们只获得了合并样本,并希望进行因果效应估计。使用 OverRule 表征支持/重叠区域后,我们现在可以过滤数据并在缩减后的数据集上进行分析。
[43]:
# Note that we are using the filtered_df here
model = CausalModel(
data = filtered_df,
treatment='treat',
outcome='re78',
common_causes="nodegr+black+hisp+age+educ+married+re74+re75".split("+")
)
identified_estimand = model.identify_effect(proceed_when_unidentifiable=True)
estimate = model.estimate_effect(identified_estimand,
method_name="backdoor.propensity_score_weighting",
target_units="ate",
method_params={"weighting_scheme":"ips_weight"})
print("Causal Estimate is " + str(estimate.value))
Causal Estimate is -958.9002273474416
免责声明:这仅是说明如何将 OverRule 纳入因果推断工作流程的示例。然而,任务本身有点人工:在这里,我们合并了实验数据(来自 Lalonde)和观测数据(来自 PSID),这可能会给我们的估计带来偏差。我们在此这样做仅是为了证明 OverRule 可以识别合并样本中处理和对照之间缺乏重叠的情况。