对 Lalonde 和 IHDP 数据集应用反驳测试#

导入依赖项#

[1]:

import dowhy
from dowhy import CausalModel
import pandas as pd
import numpy as np

# Config dict to set the logging level
import logging.config
DEFAULT_LOGGING = {
    'version': 1,
    'disable_existing_loggers': False,
    'loggers': {
        '': {
            'level': 'WARN',
        },
    }
}

logging.config.dictConfig(DEFAULT_LOGGING)
# Disabling warnings output
import warnings
from sklearn.exceptions import DataConversionWarning
warnings.filterwarnings(action='ignore', category=DataConversionWarning)

加载数据集#

婴儿健康和发展计划数据集 (IHDP)#

使用的测量指标包括：儿童的出生体重、头围、早产周数、出生顺序、是否头胎、新生儿健康指数（参见 Scott 和 Bauer 1989）、性别、是否双胞胎——以及母亲在怀孕期间的行为——是否吸烟、饮酒、服药——以及母亲在分娩时的测量指标——年龄、婚姻状况、教育程度（未高中毕业、高中毕业、上过大学但未毕业、大学毕业）、怀孕期间是否工作、是否接受产前护理——以及家庭开始干预时所在的地点（共 8 个）。数据包含 6 个连续协变量和 19 个二元协变量。

参考文献#

Hill, J. L. (2011). Bayesian nonparametric modeling for causal inference. Journal of Computational and Graphical Statistics, 20(1), 217-240. https://doi.org/10.1198/jcgs.2010.08162

[2]:

data = pd.read_csv("https://raw.githubusercontent.com/AMLab-Amsterdam/CEVAE/master/datasets/IHDP/csv/ihdp_npci_1.csv", header = None)
col =  ["treatment", "y_factual", "y_cfactual", "mu0", "mu1" ,]
for i in range(1,26):
    col.append("x"+str(i))
data.columns = col
data = data.astype({"treatment":'bool'}, copy=False)
data.head()

[2]:
treatment y_factual y_cfactual mu0 mu1 x1 x2 x3 x4 x5 ... x16 x17 x18 x19 x20 x21 x22 x23 x24 x25
0 True 5.599916 4.318780 3.268256 6.854457 -0.528603 -0.343455 1.128554 0.161703 -0.316603 ... 1 1 1 1 0 0 0 0 0 0
1 False 6.875856 7.856495 6.636059 7.562718 -1.736945 -1.802002 0.383828 2.244320 -0.629189 ... 1 1 1 1 0 0 0 0 0 0
2 False 2.996273 6.633952 1.570536 6.121617 -0.807451 -0.202946 -0.360898 -0.879606 0.808706 ... 1 0 1 1 0 0 0 0 0 0
3 False 1.366206 5.697239 1.244738 5.889125 0.390083 0.596582 -1.850350 -0.879606 -0.004017 ... 1 0 1 1 0 0 0 0 0 0
4 False 1.963538 6.202582 1.685048 6.191994 -1.045229 -0.602710 0.011465 0.161703 0.683672 ... 1 1 1 1 0 0 0 0 0 0

5 行 × 30 列

Lalonde 数据集#

一个包含 445 个观测值和以下 12 个变量的数据框。

  • age：年龄（岁）。

  • educ：受教育年限。

  • black：黑人指示变量。

  • hisp：西班牙裔指示变量。

  • married：婚姻状况指示变量。

  • nodegr：高中毕业文凭指示变量。

  • re74：1974 年实际收入。

  • re75：1975 年实际收入。

  • re78：1978 年实际收入。

  • u74：1974 年收入为零的指示变量。

  • u75：1975 年收入为零的指示变量。

  • treat：治疗状态的指示变量。

参考文献#

Dehejia, Rajeev and Sadek Wahba. 1999.``Causal Effects in Non-Experimental Studies: Re-Evaluating the Evaluation of Training Programs.’’ Journal of the American Statistical Association 94 (448): 1053-1062.

LaLonde, Robert. 1986. ``Evaluating the Econometric Evaluations of Training Programs.’’ American Economic Review 76:604-620.

[3]:

import dowhy.datasets

lalonde = dowhy.datasets.lalonde_dataset()

lalonde.head()

[3]:
treat age educ black hisp married nodegr re74 re75 re78 u74 u75
0 False 23.0 10.0 1.0 0.0 0.0 1.0 0.0 0.0 0.00 1.0 1.0
1 False 26.0 12.0 0.0 0.0 0.0 0.0 0.0 0.0 12383.68 1.0 1.0
2 False 22.0 9.0 1.0 0.0 0.0 1.0 0.0 0.0 0.00 1.0 1.0
3 False 18.0 9.0 1.0 0.0 0.0 1.0 0.0 0.0 10740.08 1.0 1.0
4 False 45.0 11.0 1.0 0.0 0.0 1.0 0.0 0.0 11796.47 1.0 1.0

步骤 1：构建模型#

IHDP#

[4]:

# Create a causal model from the data and given common causes

common_causes = []

for i in range(1, 26):
    common_causes += ["x"+str(i)]

ihdp_model = CausalModel(
                data=data,
                treatment='treatment',
                outcome='y_factual',
                common_causes=common_causes
            )
ihdp_model.view_model(layout="dot")
from IPython.display import Image, display
display(Image(filename="causal_model.png"))
../_images/example_notebooks_dowhy_refutation_testing_12_0.png
../_images/example_notebooks_dowhy_refutation_testing_12_1.png

Lalonde#

[5]:

lalonde_model = CausalModel(
                data=lalonde,
                treatment='treat',
                outcome='re78',
                common_causes='nodegr+black+hisp+age+educ+married'.split('+')
            )
lalonde_model.view_model(layout="dot")
from IPython.display import Image, display
display(Image(filename="causal_model.png"))
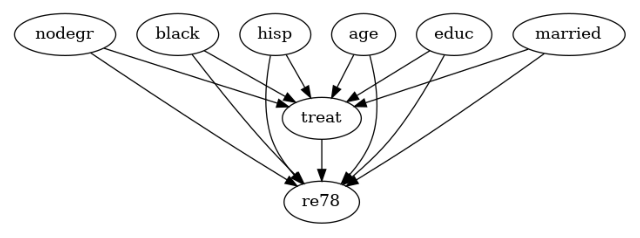
../_images/example_notebooks_dowhy_refutation_testing_14_0.png
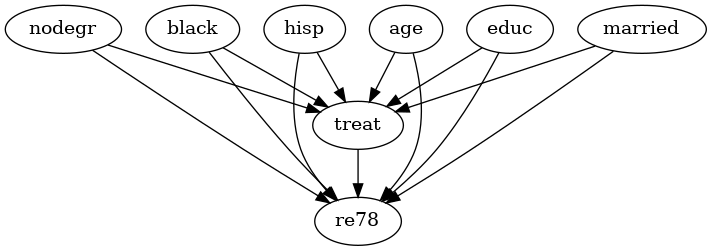
../_images/example_notebooks_dowhy_refutation_testing_14_1.png

步骤 2：识别#

IHDP#

[6]:

#Identify the causal effect for the ihdp dataset
ihdp_identified_estimand = ihdp_model.identify_effect(proceed_when_unidentifiable=True)
print(ihdp_identified_estimand)

Estimand type: EstimandType.NONPARAMETRIC_ATE

### Estimand : 1
Estimand name: backdoor
Estimand expression:
     d                                                                         ↪
────────────(E[y_factual|x25,x21,x12,x6,x18,x3,x15,x16,x8,x4,x11,x2,x24,x17,x2 ↪
d[treatment]                                                                   ↪

↪
↪ 3,x7,x9,x5,x22,x13,x19,x1,x20,x10,x14])
↪
Estimand assumption 1, Unconfoundedness: If U→{treatment} and U→y_factual then P(y_factual|treatment,x25,x21,x12,x6,x18,x3,x15,x16,x8,x4,x11,x2,x24,x17,x23,x7,x9,x5,x22,x13,x19,x1,x20,x10,x14,U) = P(y_factual|treatment,x25,x21,x12,x6,x18,x3,x15,x16,x8,x4,x11,x2,x24,x17,x23,x7,x9,x5,x22,x13,x19,x1,x20,x10,x14)

### Estimand : 2
Estimand name: iv
No such variable(s) found!

### Estimand : 3
Estimand name: frontdoor
No such variable(s) found!

Lalonde#

[7]:

#Identify the causal effect for the lalonde dataset
lalonde_identified_estimand = lalonde_model.identify_effect(proceed_when_unidentifiable=True)
print(lalonde_identified_estimand)

Estimand type: EstimandType.NONPARAMETRIC_ATE

### Estimand : 1
Estimand name: backdoor
Estimand expression:
   d
────────(E[re78|age,nodegr,educ,married,black,hisp])
d[treat]
Estimand assumption 1, Unconfoundedness: If U→{treat} and U→re78 then P(re78|treat,age,nodegr,educ,married,black,hisp,U) = P(re78|treat,age,nodegr,educ,married,black,hisp)

### Estimand : 2
Estimand name: iv
No such variable(s) found!

### Estimand : 3
Estimand name: frontdoor
No such variable(s) found!

步骤 3：估计 (使用倾向评分加权)#

IHDP#

[8]:

ihdp_estimate = ihdp_model.estimate_effect(
                    ihdp_identified_estimand,
                    method_name="backdoor.propensity_score_weighting"
                )

print("The Causal Estimate is " + str(ihdp_estimate.value))

The Causal Estimate is 4.028748218389962

Lalonde#

[9]:

lalonde_estimate = lalonde_model.estimate_effect(
                        lalonde_identified_estimand,
                        method_name="backdoor.propensity_score_weighting"
                    )

print("The Causal Estimate is " + str(lalonde_estimate.value))

The Causal Estimate is 1639.8089610946918

步骤 4：反驳#

IHDP#

添加随机共同原因#

[10]:

ihdp_refute_random_common_cause = ihdp_model.refute_estimate(
                                        ihdp_identified_estimand,
                                        ihdp_estimate,
                                        method_name="random_common_cause"
                                    )

print(ihdp_refute_random_common_cause)

Refute: Add a random common cause
Estimated effect:4.028748218389962
New effect:4.028748218389964
p value:1.0

用安慰剂替换治疗#

[11]:

ihdp_refute_placebo_treatment = ihdp_model.refute_estimate(
                                    ihdp_identified_estimand,
                                    ihdp_estimate,
                                    method_name="placebo_treatment_refuter",
                                    placebo_type="permute"
                                )

print(ihdp_refute_placebo_treatment)

Refute: Use a Placebo Treatment
Estimated effect:4.028748218389962
New effect:-0.4415444471465237
p value:0.02

移除随机数据子集#

[12]:

ihdp_refute_random_subset = ihdp_model.refute_estimate(
                                    ihdp_identified_estimand,
                                    ihdp_estimate,
                                    method_name="data_subset_refuter",
                                    subset_fraction=0.8
                            )
print(ihdp_refute_random_subset)

Refute: Use a subset of data
Estimated effect:4.028748218389962
New effect:4.03306148112277
p value:0.96

Lalonde#

添加随机共同原因#

[13]:

lalonde_refute_random_common_cause = lalonde_model.refute_estimate(
                                            lalonde_identified_estimand,
                                            lalonde_estimate,
                                            method_name="random_common_cause"
                                        )

print(lalonde_refute_random_common_cause)

Refute: Add a random common cause
Estimated effect:1639.8089610946918
New effect:1639.8089610946924
p value:1.0

用安慰剂替换治疗#

[14]:

lalonde_refute_placebo_treatment = lalonde_model.refute_estimate(
                                        lalonde_identified_estimand,
                                        lalonde_estimate,
                                        method_name="placebo_treatment_refuter",
                                        placebo_type="permute"
                                    )

print(lalonde_refute_placebo_treatment)

Refute: Use a Placebo Treatment
Estimated effect:1639.8089610946918
New effect:-156.25759930326174
p value:0.82

移除随机数据子集#

[15]:

lalonde_refute_random_subset = lalonde_model.refute_estimate(
                                    lalonde_identified_estimand,
                                    lalonde_estimate,
                                    method_name="data_subset_refuter",
                                    subset_fraction=0.9
                                )

print(lalonde_refute_random_subset)

Refute: Use a subset of data
Estimated effect:1639.8089610946918
New effect:1656.1546989508256
p value:0.8600000000000001