401(k) 资格对净金融资产的影响#

在此案例研究中，我们将使用来自 401(k) 分析的真实世界数据，解释如何使用图因果模型估计平均处理效应 (ATE) 和条件平均处理效应 (CATE)。

背景#

20世纪80年代初，美国政府为雇员引入了几种税收递延储蓄方案，以鼓励个人为退休进行储蓄。其中一种流行的方案是 401(k) 计划，该计划允许雇员将一部分工资存入个人账户。本研究的目标是理解 401(k) 资格对净金融资产（即 401(k) 余额与非 401(k) 资产的总和）的影响，同时考虑个体特征（特别是收入）造成的异质性。

由于 401(k) 计划由雇主提供，只有提供此类计划的公司的雇员才有资格参与。因此，我们正在处理的是一项非随机化研究。有几个因素（例如教育程度、储蓄偏好）会影响 401(k) 资格以及净金融资产。

数据#

我们考虑了 1991 年收入和计划参与调查 (Survey of Income and Program Participation) 的一个样本。该样本包括参考个体年龄在 25-64 岁之间，且至少有一名个体受雇但无人个体经营的家庭。样本中有 9915 个家庭记录。每个家庭记录了 44 个变量，其中包括户主是否符合 401(k) 计划资格（处理）、净金融资产（结果），以及其他协变量，如年龄、收入、家庭规模、教育程度、婚姻状况等。我们特别考虑了其中的 16 个协变量。

下表总结了本案例研究中使用的变量。

变量名称

类型

详情

e401

处理

401(k) 计划资格

net_tfa

结果

净金融资产（美元）

age

协变量

年龄

inc

协变量

收入（美元）

fsize

协变量

家庭规模

educ

协变量

教育年限

male

协变量

是否男性?

db

协变量

固定收益养老金

marr

协变量

是否已婚?

twoearn

协变量

双职工家庭

pira

协变量

参与 IRA

hown

协变量

是否房主?

hval

协变量

房屋价值（美元）

hequity

协变量

房屋净值（美元）

hmort

协变量

房屋抵押贷款（美元）

nohs

协变量

未上高中？（独热编码）

hs

协变量

高中毕业？（独热编码）

smcol

协变量

上过大学？（独热编码）

该数据集可从 `hdm <https://rdrr.io/cran/hdm/man/pension.html>`__ R 软件包在线公开获取。有关数据集的更多详细信息，请参阅以下论文

  1. Chernohukov, C. Hansen (2004). 401(k) 参与对财富分布的影响：工具变量分位数回归分析。《经济与统计评论》86 (3), 735–751。

首先加载并分析数据。

[1]:

import pandas as pd
df = pd.read_csv("pension.csv")

[2]:

df.head()

[2]:
ira a401 hval hmort hequity nifa net_nifa tfa net_tfa tfa_he ... i3 i4 i5 i6 i7 a1 a2 a3 a4 a5
0 0 0 69000 60150 8850 100 -3300 100 -3300 5550 ... 1.0 0.0 0.0 0.0 0.0 0.0 1.0 0.0 0.0 0.0
1 0 0 78000 20000 58000 61010 61010 61010 61010 119010 ... 0.0 1.0 0.0 0.0 0.0 0.0 0.0 0.0 1.0 0.0
2 1800 0 200000 15900 184100 7549 7049 9349 8849 192949 ... 0.0 0.0 0.0 1.0 0.0 0.0 0.0 0.0 1.0 0.0
3 0 0 0 0 0 2487 -6013 2487 -6013 -6013 ... 0.0 0.0 1.0 0.0 0.0 1.0 0.0 0.0 0.0 0.0
4 0 0 300000 90000 210000 10625 -2375 10625 -2375 207625 ... 0.0 1.0 0.0 0.0 0.0 0.0 0.0 1.0 0.0 0.0

5 行 × 44 列

401(k) 资格对净金融资产的影响（基于收入的条件分析）#

首先，我们构建一个因果图，包括 401(k) 计划资格（处理 \(T\)）、净金融资产（结果 \(Y\)）、我们假设能阻断 \(Y\) 和 \(T\) 之间所有后门路径的控制变量 \(W\)，以及收入 \(X\)（我们希望基于此研究处理效应异质性的协变量）。

[3]:

import networkx as nx
import dowhy.gcm as gcm

treatment_var = "e401"
outcome_var = "net_tfa"
covariates = ["age","inc","fsize","educ","male","db",
              "marr","twoearn","pira","hown","hval",
              "hequity","hmort","nohs","hs","smcol"]

edges = [(treatment_var, outcome_var)]
edges.extend([(covariate, treatment_var) for covariate in covariates])
edges.extend([(covariate, outcome_var) for covariate in covariates])

# To ensure that the treatment is considered as a categorical variable, we convert the values explicitly to strings.
df = df.astype({treatment_var: str})

causal_graph = nx.DiGraph(edges)

[4]:

from dowhy.utils import plot

plot(causal_graph, figure_size=[20, 20])
../_images/example_notebooks_gcm_401k_analysis_7_0.png

这里我们创建了一个简化图，其中协变量之间（即 \(X \cup W\) 中的节点）没有相互作用。在实践中，这很可能不是实际情况。然而，由于我们稍后直接从观测数据中获取协变量的联合样本来估计 CATE，我们可以忽略它们之间的相互作用。

在将因果模型分配给变量之前，我们先绘制它们的直方图，了解变量的分布情况。

[5]:

import matplotlib.pyplot as plt

cols = [treatment_var, outcome_var]
cols.extend(covariates)
plt.figure(figsize=(10,5))
for i, col in enumerate(cols):
    plt.subplot(3,6,i+1)
    plt.grid(False)
    plt.hist(df[col])
    plt.xlabel(col)
plt.tight_layout()
plt.show()
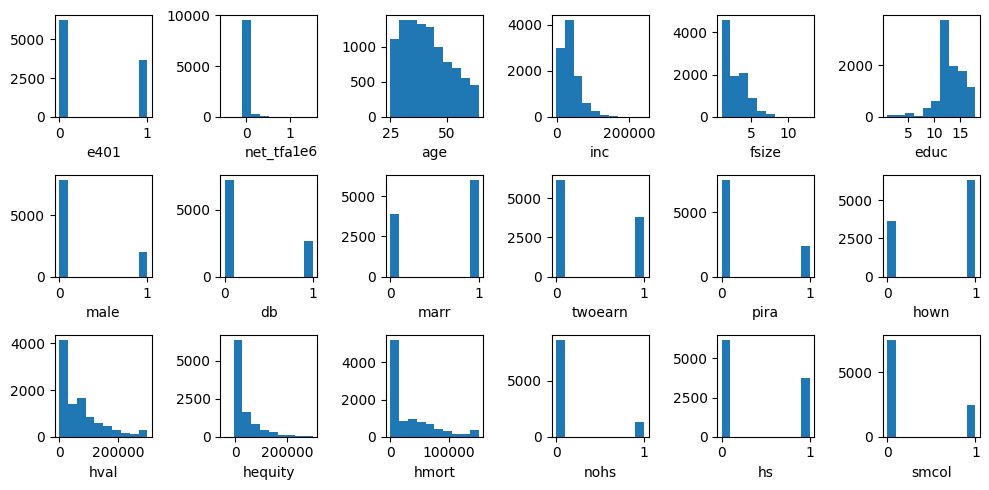
../_images/example_notebooks_gcm_401k_analysis_9_0.png

我们观察到实值变量不遵循诸如高斯分布等已知的参数分布。因此，对于没有父节点的变量，我们拟合经验分布，这对于分类变量也适用。

让我们明确地为每个节点分配因果机制。对于处理变量，我们使用随机森林分类器分配一个分类器函数式因果模型 (FCM)。对于结果变量，我们使用随机森林回归作为函数并为噪声分配经验分布，来分配一个加性噪声模型。由于因果图中其他变量没有父节点，我们为其分配经验分布。

[6]:

causal_model = gcm.StructuralCausalModel(causal_graph)
causal_model.set_causal_mechanism(treatment_var, gcm.ClassifierFCM(gcm.ml.create_random_forest_classifier()))
causal_model.set_causal_mechanism(outcome_var, gcm.AdditiveNoiseModel(gcm.ml.create_random_forest_regressor()))
for covariate in covariates:
    causal_model.set_causal_mechanism(covariate, gcm.EmpiricalDistribution())

如果我们没有先验知识或不熟悉统计学含义，也可以使用启发式方法自动分配因果机制

gcm.auto.assign_causal_mechanisms(causal_model, df)

这样，我们现在就可以从数据中拟合学习因果模型了。

[7]:

gcm.fit(causal_model, df)

Fitting causal mechanism of node smcol: 100%|██████████| 18/18 [00:06<00:00,  2.67it/s]

在计算 CATE 之前，我们首先将家庭按照收入百分位数划分为等宽的区间。这使得我们能够研究对不同收入群体的影响。

[8]:

import numpy as np

percentages = [0.0, 0.2, 0.4, 0.6, 0.8, 1.0]
bin_edges = [0]
bin_edges.extend(np.quantile(df.inc, percentages[1:]).tolist())
bin_edges[-1] += 1 # adding 1 to the last edge as last edge is excluded by np.digitize

groups = [f'{percentages[i]*100:.0f}%-{percentages[i+1]*100:.0f}%' for i in range(len(percentages)-1)]
group_index_to_group_label = dict(zip(range(1, len(bin_edges)+1), groups))

现在我们可以计算 CATE 了。为此，我们在已拟合的因果图中对处理变量进行随机干预，从干预分布中抽取样本，按收入组对观测结果进行分组，然后计算每组的处理效应。

[9]:

np.random.seed(47)

def estimate_cate():
    samples = gcm.interventional_samples(causal_model,
                                         {treatment_var: lambda x: np.random.choice(['0', '1'])},
                                         observed_data=df)
    eligible = samples[treatment_var] == '1'
    ate = samples[eligible][outcome_var].mean() - samples[~eligible][outcome_var].mean()
    result = dict(ate = ate)

    group_indices = np.digitize(samples['inc'], bin_edges)
    samples['group_index'] = group_indices

    for group_index in group_index_to_group_label:
        group_samples = samples[samples['group_index'] == group_index]
        eligible_in_group = group_samples[treatment_var] == '1'
        cate = group_samples[eligible_in_group][outcome_var].mean() - group_samples[~eligible_in_group][outcome_var].mean()
        result[group_index_to_group_label[group_index]] = cate

    return result

group_to_median, group_to_ci = gcm.confidence_intervals(estimate_cate, num_bootstrap_resamples=100)
print(group_to_median)
print(group_to_ci)

Estimating bootstrap interval...: 100%|██████████| 100/100 [00:43<00:00,  2.32it/s]

{'ate': 6524.583223183401, '0%-20%': 4010.8760624539045, '20%-40%': 3124.591365845997, '40%-60%': 5479.491988474934, '60%-80%': 7622.045252631407, '80%-100%': 12235.611495154653}
{'ate': array([4912.93938262, 8465.43365925]), '0%-20%': array([2612.44786522, 5582.21766875]), '20%-40%': array([1187.57446995, 5164.17566841]), '40%-60%': array([3333.67563274, 8129.58879172]), '60%-80%': array([ 4696.03425313, 10738.80810366]), '80%-100%': array([ 5083.79029031, 18774.95557817])}





401(k) 资格对净金融资产的平均处理效应是正向的，这由相应的置信区间表明。现在，让我们绘制不同收入组的 CATE 图，以便更清晰地了解情况。




[10]:





fig = plt.figure(figsize=(8,4))
for x, group in enumerate(groups):
    ci = group_to_ci[group]
    plt.plot((x, x), (ci[0], ci[1]), 'ro-', color='orange')
ax = fig.axes[0]
ax.spines['right'].set_visible(False)
ax.spines['top'].set_visible(False)
plt.xticks(range(len(groups)), groups)
plt.xlabel('Income group')
plt.ylabel('ATE of 401(k) eligibility on net financial assets')
plt.show()















/tmp/ipykernel_4333/1344202636.py:4: UserWarning: color is redundantly defined by the 'color' keyword argument and the fmt string "ro-" (-> color='r'). The keyword argument will take precedence.
  plt.plot((x, x), (ci[0], ci[1]), 'ro-', color='orange')












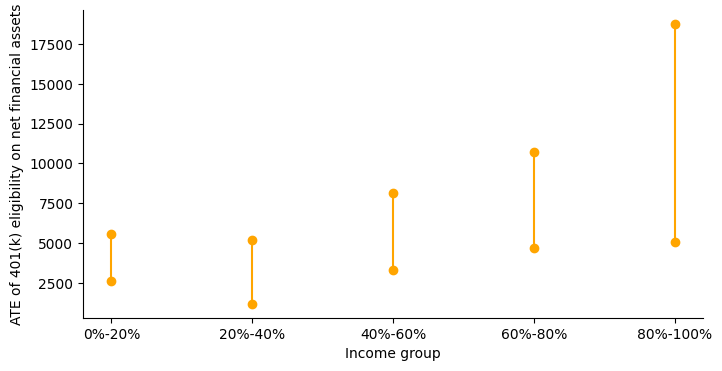
../_images/example_notebooks_gcm_401k_analysis_20_1.png





随着收入从低到高变化，影响也随之增加。这一结果似乎与不同收入群体的资源限制相符。